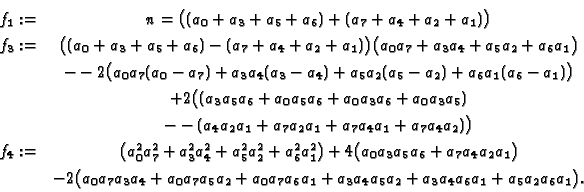Die Gleichungen
Sei ![]() der Expositionsfaktor (proportionaler Anteil der Kinder, die durch
die Krankheit
der Expositionsfaktor (proportionaler Anteil der Kinder, die durch
die Krankheit ![]() Antikörper zur Krankheit
Antikörper zur Krankheit ![]() haben),
haben), ![]() der
proportionale Anteil der Kinder, die erfolgreich gegen die Krankheit
der
proportionale Anteil der Kinder, die erfolgreich gegen die Krankheit ![]() geimpft wurden und
geimpft wurden und
![]() der proportionale Anteil der Kinder
mit Antikörper zur Krankheit
der proportionale Anteil der Kinder
mit Antikörper zur Krankheit ![]() , die geimpft worden sind.
, die geimpft worden sind.
Sei
![]() mit
mit ![]() (bzw.
(bzw. ![]() ) an der
) an der ![]() -ten Stelle der
proportinalen Anteil der Kinder, die Antikörper (bzw. keine Antikörper) zur
-ten Stelle der
proportinalen Anteil der Kinder, die Antikörper (bzw. keine Antikörper) zur
![]() -ten Krankheit haben. Die acht Werte
-ten Krankheit haben. Die acht Werte
![]() sind durch die Labors bekannt. Man hat die folgende Gleichungen:
sind durch die Labors bekannt. Man hat die folgende Gleichungen:
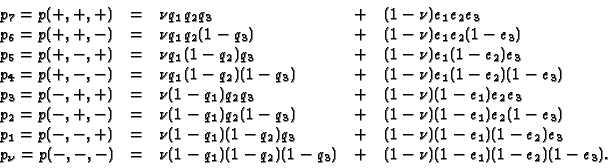
Nach der (technischen) Substitution
Mit Hilfe der Faktorisierung von SINGULAR erhält man
Daraus gewinnt man die Formeln
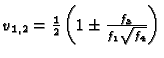 mit
mit