|
|
D.4.18.10 intersectionValRingIdeals
Procedure from library normaliz.lib (see normaliz_lib).
- Usage:
- intersectionValRingIdeals(intmat V);
intersectionValRingIdeals(intmat V, intvec grading);
- Return:
- The function returns two ideals, both to be considered as lists of
monomials. The
first is the system of monomial generators of
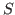 , the second
the system of generators of , the second
the system of generators of
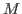 . .
The function returns a list consisting of the ideal given by the
input matrix T if one of the options supp, triang, or
hvect has been activated.
However, in this case some numerical invariants are computed, and
some other data may be contained in files that you can read into
Singular (see showNuminvs, exportNuminvs).
- Background:
- A discrete monomial valuation
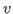 on on
![$R = K[X_1 ,\ldots,X_n]$](sing_1047.png) is determined by
the values is determined by
the values 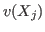 of the indeterminates. This function computes the
subalgebra of the indeterminates. This function computes the
subalgebra
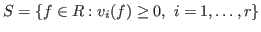 for several
such valuations for several
such valuations 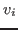 , ,  . It needs the matrix . It needs the matrix
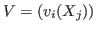 as
its input. as
its input.
This function simultaneously determines the 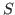 -submodule -submodule
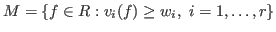 for integers for integers
 . (If . (If  for all for all 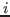 , , 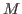 is an ideal of is an ideal of 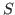 .)
The numbers .)
The numbers 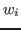 form the form the 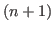 th column of the input matrix. th column of the input matrix.
- Note:
- The function also gives an error message if the matrix V has the
wrong number of columns.
Example:
| | LIB "normaliz.lib";
ring R=0,(x,y,z,w),dp;
intmat V[2][5]=0,1,2,3,4, -1,1,2,1,3;
intersectionValRingIdeals(V);
==> [1]:
==> _[1]=y
==> _[2]=xy
==> _[3]=w
==> _[4]=xw
==> _[5]=z
==> _[6]=xz
==> _[7]=x2z
==> [2]:
==> _[1]=zw
==> _[2]=z2
==> _[3]=xz2
==> _[4]=y2w
==> _[5]=y2z
==> _[6]=xy2z
==> _[7]=y4
==> _[8]=xy4
==> _[9]=yw2
==> _[10]=w3
|
See also:
diagInvariants;
finiteDiagInvariants;
intersectionValRings;
torusInvariants.
|