|
|
5.1.4 betti
Syntax:
betti ( list_expression )
betti ( resolution_expression )
betti ( list_expression , int_expression )
betti ( resolution_expression , int_expression )
Type:
- intmat
Purpose:
- with 1 argument: computes the graded Betti numbers of a minimal resolution of
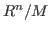 , if , if 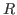 denotes the basering, denotes the basering,
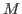 is a homogeneous submodule of is a homogeneous submodule of 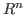 and the argument represents a
resolution of and the argument represents a
resolution of
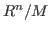 . .
The entry d of the intmat at place (i,j) is the minimal number of
generators in degree i+j of the j-th syzygy module (= module of
relations) of 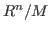 , i.e. the 0th (resp. 1st) syzygy module of , i.e. the 0th (resp. 1st) syzygy module of 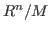 is is
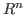 (resp. (resp. 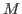 ).The argument is considered to be the result of a res/sres/mres/nres/lres
command. This implies that a zero is only allowed (and counted) as a
generator in the first module. ).The argument is considered to be the result of a res/sres/mres/nres/lres
command. This implies that a zero is only allowed (and counted) as a
generator in the first module.
For the computation betti uses only the initial monomials. This could lead
to confusing results for a non-homogeneous input.
If the optional second argument is non-zero, the Betti numbers will be minimized.
Example:
| | ring r=32003,(a,b,c,d),dp;
ideal j=bc-ad,b3-a2c,c3-bd2,ac2-b2d;
list T=mres(j,0); // 0 forces a full resolution
// a minimal set of generators for j:
print(T[1]);
==> bc-ad,
==> c3-bd2,
==> ac2-b2d,
==> b3-a2c
// second syzygy module of r/j which is the first
// syzygy module of j (minimal generating set):
print(T[2]);
==> bd,c2,ac,b2,
==> -a,-b,0, 0,
==> c, d, -b,-a,
==> 0, 0, -d,-c
// the second syzygy module (minimal generating set):
print(T[3]);
==> -b,
==> a,
==> -c,
==> d
print(T[4]);
==> 0
betti(T);
==> 1,0,0,0,
==> 0,1,0,0,
==> 0,3,4,1
// most useful for reading off the graded Betti numbers:
print(betti(T),"betti");
==> 0 1 2 3
==> ------------------------------
==> 0: 1 - - -
==> 1: - 1 - -
==> 2: - 3 4 1
==> ------------------------------
==> total: 1 4 4 1
==>
|
Hence,
- the 0th syzygy module of r/j (which is r) has 1 generator in
degree 0 (which is 1),
- the 1st syzygy module
T[1] (which is j) has 4
generators (one in degree 2 and three in degree 3),
- the 2nd syzygy
module
T[2] has 4 generators (all in degree 4),
- the 3rd syzygy module
T[3] has
1 generator in degree 5,
where the generators are the columns of the
displayed matrix and degrees are assigned such that the corresponding maps
have degree 0:
See
Syzygies and resolutions;
hres;
lres;
mres;
print;
res;
resolution;
sres.
|