|
|
3.3.2 General syntax of a ring declaration
Rings
- Syntax:
ring name = (coefficients),
( names_of_ring_variables ),
( ordering );
- Default:
32003,(x,y,z),(dp,C);
- Purpose:
- declares a ring and sets it as the current basering.
The coefficients are given by one of the following:
-
a non-negative int_expression less than 2147483648 (2^31).
The int_expression should either be 0, specifying the field of
rational numbers Q, or a prime number p, specifying the finite field
with p elements. If it is not a prime number, int_expression is
converted to the next lower prime number.
-
an expression_list of an int_expression and one or more names.
The int_expression specifies the characteristic of the coefficient
field as described above. The names are used as parameters in
transcendental or algebraic extensions of the coefficient
field. Algebraic extensions are implemented for one parameter only. In
this case, a minimal polynomial has to be defined by an assignment to
minpoly. See minpoly.
-
an expression_list of an int_expression and a name.
The int_expression has to be a prime number p to the power of a
positive integer n. This defines the Galois field
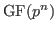 with with 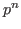 elements, where elements, where 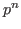 has to be less than or equal to has to be less than or equal to 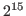 .The given name refers to a primitive element of .The given name refers to a primitive element of
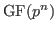 generating the multiplicative group. Due to a different internal
representation, the arithmetic operations in these coefficient fields
are faster than arithmetic operations in algebraic extensions as
described above. generating the multiplicative group. Due to a different internal
representation, the arithmetic operations in these coefficient fields
are faster than arithmetic operations in algebraic extensions as
described above.
-
an expression_list of the name
real and two optional int_expressions
determining the precision in decimal digits and
the size for the stabilizing rest. The default for the rest is the same size
as for the representation.
An exeption is the name real without any integers.
These numbers are implemented as machine floating point numbers
of single precision.
Note that computations over all these fields are not exact.
-
an expression_list of the name
complex,
two optional int_expression and a name.
This specifies the field of complex numbers represented by floating point
numbers with a precision similar to real. An expression_list
without int_expression defines a precision and rest with length 6.
The name of the imaginary unit is given by the last parameter.
Note that computations over these fields are not exact.
-
an expression_list with the name
integer. This specifies the ring of integers.
-
an expression_list with the name
integer and one subsequent int_expression.
This specifies the ring of integers modulo the given int_expression.
-
an expression_list with the name
integer and two int_expressions b and e.
This specifies the ring of integers modulo b^e. If b = 2 and e < int_bit_size
an optimized implementation is used.
'names_of_ring_variables' is a list of names or indexed names.
'ordering' is a list of block orderings where each block ordering is either
-
lp, dp, Dp, ls, ds, or Ds
optionally followed by a size parameter in parentheses.
-
wp, Wp, ws, Ws, or a followed by a
weight vector given as an intvec_expression in parentheses.
-
M followed by an intmat_expression in parentheses.
-
c or C.
For the definition of the orderings, see Monomial orderings.
If one of coefficients, names_of_ring_variables, and ordering
consists of only one entry, the parentheses around this entry may be
omitted.
Quotient rings
- Syntax:
qring name = ideal_expression ;
- Default:
- none
- Purpose:
- declares a quotient ring as the basering modulo ideal_expression, and sets
it as current basering.
ideal_expression has to be represented by a standard basis.
The most convenient way to map objects from a ring to its quotient ring
and vice versa is to use the fetch function (see fetch).
SINGULAR computes in a quotient ring as long as possible with the
given representative of a polynomial, say, f. I.e., it usually
does not reduce f w.r.t. the quotient ideal. This is only done
when necessary
during standard bases computations or by an explicit reduction using
the command reduce(f, std(0)) (see reduce).
Operations based on standard bases (e.g. std,groebner, etc., reduce) and functions which require a standard basis (e.g. dim,hilb, etc.) operated with the residue classes; all others on the polynomial objects.
Example:
| | // defintion and usage:
ring r=32003,(x,y),dp;
poly f=x3+yx2+3y+4;
qring q=std(maxideal(2));
basering;
==> // characteristic : 32003
==> // number of vars : 2
==> // block 1 : ordering dp
==> // : names x y
==> // block 2 : ordering C
==> // quotient ring from ideal
==> _[1]=y2
==> _[2]=xy
==> _[3]=x2
poly g=fetch(r, f);
g;
==> x3+x2y+3y+4
reduce(g,std(0));
==> 3y+4
// polynomial and residue class:
ring R=0,(x,y),dp;
qring Q=std(y);
poly p1=x;
poly p2=x+y;
// comparing polynomial objects:
p1==p2;
==> 0
// comparing residue classes:
reduce(p1,std(0))==reduce(p2,std(0));
==> 1
|
|
 Online Manual
Online Manual