|
|
7.3.15 mres (plural)
Syntax:
mres ( ideal_expression, int_expression )
mres ( module_expression, int_expression )
Type:
- resolution
Purpose:
- computes a minimal free resolution of an ideal or module M with the
Groebner basis method. More precisely, let A=
matrix(M), then mres
computes a free resolution of
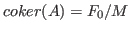
where the columns of the matrix
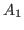 are a (possibly) minimal set of generators
of are a (possibly) minimal set of generators
of
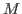 .
If the int expression k is not zero, then the computation stops after k steps
and returns a resolution consisting of modules .
If the int expression k is not zero, then the computation stops after k steps
and returns a resolution consisting of modules
 , , 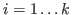 . .
mres(M,0) returns a resolution consisting of at most n+2 modules,
where n is the number of variables of the basering.
Let list L=mres(M,0);
then L[1] consists of a minimal set of generators M, L[2]
consists of a minimal set of generators for the first syzygy module of
L[1], etc., until L[p+1], such that
![${\tt L[i]}\neq 0$](sing_166.png) for for 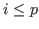 , but , but L[p+1] (the first syzygy module of L[p])
is 0 (if the basering is not a qring).
Note:
- Accessing single elements of a resolution may require that some partial
computations have to be finished and may therefore take some time. Hence, assigning right away to a list
is the recommended way to do it.
Example:
| | LIB "ncalg.lib";
def A = makeUsl2();
setring A; // this algebra is U(sl_2)
option(redSB);
option(redTail);
ideal i = e,f,h;
i = std(i);
resolution M=mres(i,0);
M;
==> 1 2 2 1
==> A <-- A <-- A <-- A
==>
==> 0 1 2 3
==>
list l = M; l;
==> [1]:
==> _[1]=f
==> _[2]=e
==> [2]:
==> _[1]=ef*gen(1)-f2*gen(2)-2h*gen(1)-2*gen(1)
==> _[2]=e2*gen(1)-ef*gen(2)-h*gen(2)+2*gen(2)
==> [3]:
==> _[1]=e*gen(1)-f*gen(2)
// see the exactness at this point
size(ideal(transpose(l[2])*transpose(l[1])));
==> 0
print(matrix(M[3]));
==> e,
==> -f
// see the exactness at this point
size(ideal(transpose(l[3])*transpose(l[2])));
==> 0
|
See
ideal (plural);
minres (plural);
module (plural);
nres (plural).
|