Singular

7.6.4 Example of use of LETTERPLACE

The input monomials must be given in a letterplace notation (though we recommend to get used to the letterplace notation, the procedure freeGBasis from the freegb_lib provides an alternative).

We recommend first to define a commutative ring in SINGULAR and equip it with a degree well-ordering. Then, decide what should be the degree bound d and run the procedure makeLetterplaceRing(d) from the library freegb_lib. This procedure creates a letterplace algebra with an ordering, induced from the given commutative ring . In this algebra, define an ideal I as a list of polynomials in the letterplace encoding and run the procedure letplaceGBasis. The output is given in the letterplace encoding as well.

Alternatively, one can run the procedure system("freegb",I,d,n), where 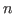is the number of variables of the original commutative ring which does the same computations as letplaceGBasis.

It is possible to convert the letterplace presentation of an ideal to a list of strings with the help of procedures lp2lstr and lst2str from the library freegb_lib. This is shown in the second part of the example below.

Yet another anternative is to use the procedure freeGBasis from freegb_lib in order to use a different encoding for polynomials in free algebra. No conversion tools are needed in that case.

We illustrate the approach with the following example:

LIB "freegb.lib";
ring r = 0,(x,y,z),dp;
int d =4; // degree bound
def R = makeLetterplaceRing(d);
setring R;
ideal I = x(1)*y(2) + y(1)*z(2), x(1)*x(2) + x(1)*y(2) - y(1)*x(2) - y(1)*y(2);
option(redSB); option(redTail);
ideal J = letplaceGBasis(I);
J;
==> J[1]=x(1)*y(2)+y(1)*z(2)
==> J[2]=x(1)*x(2)-y(1)*x(2)-y(1)*y(2)-y(1)*z(2)
==> J[3]=y(1)*y(2)*y(3)-y(1)*y(2)*z(3)+y(1)*z(2)*y(3)-y(1)*z(2)*z(3)
==> J[4]=y(1)*y(2)*x(3)+y(1)*y(2)*z(3)+y(1)*z(2)*x(3)+y(1)*z(2)*z(3)
==> J[5]=y(1)*z(2)*y(3)*y(4)-y(1)*z(2)*y(3)*z(4)+y(1)*z(2)*z(3)*y(4)-y(1)*z(2\
   )*z(3)*z(4)
==> J[6]=y(1)*z(2)*y(3)*x(4)+y(1)*z(2)*y(3)*z(4)+y(1)*z(2)*z(3)*x(4)+y(1)*z(2\
   )*z(3)*z(4)
==> J[7]=y(1)*y(2)*z(3)*y(4)-y(1)*y(2)*z(3)*z(4)+y(1)*z(2)*z(3)*y(4)-y(1)*z(2\
   )*z(3)*z(4)
==> J[8]=y(1)*y(2)*z(3)*x(4)+y(1)*y(2)*z(3)*z(4)+y(1)*z(2)*z(3)*x(4)+y(1)*z(2\
   )*z(3)*z(4)
// ----------------------------------
lp2lstr(J,r); // export an object called @code{@LN} to the ring r
setring r;  // change to the ring r
lst2str(@LN,1); // output the string presentation
==> [1]:
==>    x*y+y*z
==> [2]:
==>    x*x-y*x-y*y-y*z
==> [3]:
==>    y*y*y-y*y*z+y*z*y-y*z*z
==> [4]:
==>    y*y*x+y*y*z+y*z*x+y*z*z
==> [5]:
==>    y*z*y*y-y*z*y*z+y*z*z*y-y*z*z*z
==> [6]:
==>    y*z*y*x+y*z*y*z+y*z*z*x+y*z*z*z
==> [7]:
==>    y*y*z*y-y*y*z*z+y*z*z*y-y*z*z*z
==> [8]:
==>    y*y*z*x+y*y*z*z+y*z*z*x+y*z*z*z

There are various conversion routines in the library freegb_lib (see freegb_lib). We work further on implementing more algorithms for non-commutative ideals and modules over free associative algebra.