| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
C.8.5 Decoding method based on quadratic equations
Preliminary definitions
Let
![]() be a basis of
be a basis of ![]() and let
and let ![]() be the
be the ![]() matrix with
matrix with
![]() as rows. The unknown syndrome
as rows. The unknown syndrome
![]() of a word
of a word ![]() w.r.t
w.r.t ![]() is the column vector
is the column vector
![]() with entries
with entries
![]() for
for ![]() .
.
For two vectors
![]() define
define
![]() . Then
. Then
![]() is a linear combination of
is a linear combination of
![]() , so there are constants
, so there are constants
![]() such that
such that
![]() The elements
The elements
![]() are the structure constants of the basis
are the structure constants of the basis
![]() .
.
Let ![]() be the
be the ![]() matrix with
matrix with
![]() as rows (
as rows (![]() ).
Then
).
Then
![]() is an ordered MDS basis and
is an ordered MDS basis and ![]() an MDS matrix if all
the
an MDS matrix if all
the ![]() submatrices of
submatrices of ![]() have rank
have rank ![]() for all
for all ![]() .
.
Expressing known syndromes
Let
Let
![]() be a received word with
be a received word with ![]() and
and ![]() an error vector.
The syndromes of
an error vector.
The syndromes of ![]() and
and ![]() w.r.t
w.r.t ![]() are equal and known:
are equal and known:
They can be expressed in the unknown syndromes of
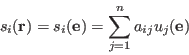
since
Contructing the system
Let ![]() be an MDS matrix with structure constants
be an MDS matrix with structure constants ![]() .
Define
.
Define ![]() in the variables
in the variables
![]() by
by
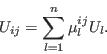
The ideal
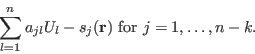
The ideal
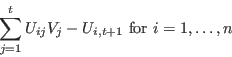
Let
Main theorem
Let ![]() be an MDS matrix with structure constants
be an MDS matrix with structure constants ![]() . Let
. Let ![]() be a check matrix of the code
be a check matrix of the code ![]() such that
such that ![]() as above.
Let
as above.
Let
![]() be a received word with
be a received word with ![]() the codeword sent
and
the codeword sent
and ![]() the error vector. Suppose that
the error vector. Suppose that
![]() and
and
![]() .
Let
.
Let ![]() be the smallest positive integer such that
be the smallest positive integer such that ![]() has a solution
has a solution ![]() over the algebraic closure of
over the algebraic closure of
![]() . Then
. Then
-
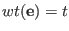 and the solution is unique and of multiplicity one satisfying
and the solution is unique and of multiplicity one satisfying
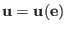 .
. -
the reduced Gröbner basis
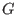 for the ideal
for the ideal 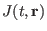 w.r.t any
monomial ordering is
w.r.t any
monomial ordering is
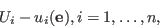
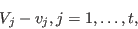
where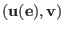 is the unique solution.
is the unique solution.
For an example see sysQE in decodegb_lib. More on this method can be found in [BP2008a].