| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
D.4.6.4 chebyshev
Procedure from librarydecomp.lib (see decomp_lib).
- Usage:
- chebyshev(n); n int, n >= 0
chebyshev(n,c); n int, n >= 0, c number, c!=0 - Return:
- poly, the [monic] nth Chebyshev polynomial of the first kind.
The polynomials are defined in the first variable, say x, of the basering. - Note:
- The (generalized) Chebyshev polynomials of the first kind can be
defined by the recursion:
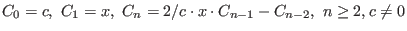 .
.These polynomials commute by composition:
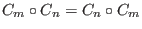 .
.
For c=1, we obtain the standard (non monic) Chebyshev polynomials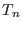 which satisfy
which satisfy
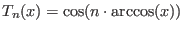 .
.
For c=2 (default), we obtain the monic Chebyshev polynomials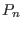
which satisfy the relation
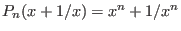 .
.
By default the monic Chebyshev polynomials are returned: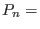
chebyshev(n)and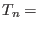
chebyshev(n,1).
It holds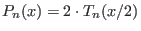 and more generally
and more generally
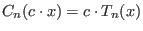
That issubst(chebyshev(n,c),var(1),c*var(1))= c*chebyshev(n,1).If
char(basering) = 2, then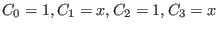 , and so on.
, and so on.
LIB "decomp.lib"; ring r = 0,x,lp; // The monic Chebyshev polynomials chebyshev(0); ==> 2 chebyshev(1); ==> x chebyshev(2); ==> x2-2 chebyshev(3); ==> x3-3x // These polynomials commute compose(chebyshev(2),chebyshev(6)) == compose(chebyshev(6),chebyshev(2)); ==> 1 // The standard Chebyshev polynomials chebyshev(0,1); ==> 1 chebyshev(1,1); ==> x chebyshev(2,1); ==> 2x2-1 chebyshev(3,1); ==> 4x3-3x // ----------------------------------------------------------------------- // The relation for the various Chebyshev polynomials 5*chebyshev(3,1)==subst(chebyshev(3,5),x,5x); ==> 1 // ----------------------------------------------------------------------- // char 2 case ring r2 = 2,x,dp; chebyshev(2); ==> 1 chebyshev(3); ==> x |