| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
3.3 Rings and orderings
All non-trivial algorithms in SINGULAR require the prior definition of a ring. Such a ring can be
- a polynomial ring over a field,
- a polynomial ring over a ring
- a localization of 1.
- a quotient ring by an ideal of 1. or 2.,
- a tensor product of 1. or 2.
Except for quotient rings, all of these rings are realized by choosing a coefficient field, ring variables, and an appropriate global or local monomial ordering on the ring variables. See Term orderings, Mathematical background.
The coefficient field of the rings may be
-
the field of rational numbers
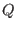 (
(QQ), -
finite fields
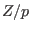 ,
, 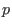 a prime
a prime
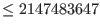 ,
, -
finite fields
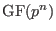 with
with 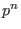 elements,
elements, 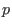 a prime,
a prime,
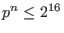 ,
, -
transcendental extension of
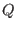 or
or
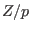 ,
,
-
simple algebraic extension of
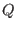 or
or
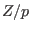 ,
,
- the field of real numbers represented by floating point numbers of a user defined precision,
- the field of complex numbers represented by (pairs of) floating point numbers of a user defined precision,
-
the ring of integers (
ZZ), -
finite rings
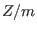 with
with
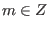 .
.
In case of coefficient rings, which are not fields (i.e.
![]() and
and
![]() ), only the following functions
are guaranteed to work:
), only the following functions
are guaranteed to work:
- - basic polynomial arithmetic, i.e. addition, multiplication, exponentiation
- - std, i.e. computing standard bases (and related: syz, etc.)
- - interred
- - reduce
Throughout this manual, the current active ring in SINGULAR is
called basering. The reserved name basering in SINGULAR is
an alias for the current active ring. The basering can be set by
declaring a new ring as described in the following subsections or by using
the commands setring and keepring. See keepring, setring.
Objects of ring dependent types are local to a ring. To access them
after a change of the basering they have to be mapped using map or by
the functions imap or fetch. See Objects, fetch,
imap, map.
All changes of the basering in a procedure are local to this procedure
unless a keepring command is used as the last statement of the
procedure. See Procedures, keepring.
3.3.1 Examples of ring declarations 3.3.2 General syntax of a ring declaration 3.3.3 Term orderings 3.3.4 Coefficient rings