|
|
5.1.130 regularity
Syntax:
regularity ( list_expression )
regularity ( resolution_expression )
Type:
- int
Purpose:
- computes the regularity of a homogeneous ideal, resp. module, from a
minimal resolution given by the argument.
Let
![$0 \rightarrow\ \bigoplus_a K[x]e_{a,n}\ \rightarrow\ \dots
\rightarrow\ \bigoplus_a K[x]e_{a,0}\ \rightarrow\
I\ \rightarrow\ 0$](sing_176.png) be a minimal resolution of I considered with homogeneous maps of degree 0.
The regularity is the smallest number
be a minimal resolution of I considered with homogeneous maps of degree 0.
The regularity is the smallest number 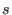 with the property deg( with the property deg(
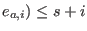 for all for all 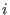 . . Note:
- If applied to a non minimal resolution only an upper bound is returned.
If the input to the commands res and mres is homogeneous
the regularity is computed and used as a degree bound during
the computation unless option(notRegularity); is given.
Example:
| | ring rh3=32003,(w,x,y,z),(dp,C);
poly f=x11+y10+z9+x5y2+x2y2z3+xy3*(y2+x)^2;
ideal j=homog(jacob(f),w);
def jr=res(j,0);
regularity(jr);
==> 25
// example for upper bound behaviour:
list jj=jr;
regularity(jj);
==> 25
jj=nres(j,0);
regularity(jj);
==> 27
jj=minres(jj);
regularity(jj);
==> 25
|
See
fres;
list;
minres;
mres;
option;
res;
resolution;
sres.
|








![$0 \rightarrow\ \bigoplus_a K[x]e_{a,n}\ \rightarrow\ \dots
\rightarrow\ \bigoplus_a K[x]e_{a,0}\ \rightarrow\
I\ \rightarrow\ 0$](sing_176.png) be a minimal resolution of I considered with homogeneous maps of degree 0.
The regularity is the smallest number
be a minimal resolution of I considered with homogeneous maps of degree 0.
The regularity is the smallest number 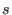 with the property deg(
with the property deg(
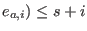 for all
for all 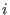 .
.