|
|
7.3.6 envelope
Syntax:
envelope ( ring_name )
Type:
- ring
Purpose:
- creates an enveloping algebra of a given algebra, that is
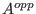 , where , where 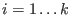 is the
opposite algebra of is the
opposite algebra of 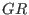 . . Remark:
- You have to activate the ring with the
setring command.
For the presentation, see explanation of opposite in opposite.
| | LIB "ncalg.lib";
def A = makeUsl2();
setring A; A;
==> // coefficients: QQ considered as a field
==> // number of vars : 3
==> // block 1 : ordering dp
==> // : names e f h
==> // block 2 : ordering C
==> // noncommutative relations:
==> // fe=ef-h
==> // he=eh+2e
==> // hf=fh-2f
def Aenv = envelope(A);
setring Aenv;
Aenv;
==> // coefficients: QQ considered as a field
==> // number of vars : 6
==> // block 1 : ordering dp
==> // : names e f h
==> // block 2 : ordering a
==> // : names H F E
==> // : weights 1 1 1
==> // block 3 : ordering ls
==> // : names H F E
==> // block 4 : ordering C
==> // noncommutative relations:
==> // fe=ef-h
==> // he=eh+2e
==> // hf=fh-2f
==> // FH=HF-2F
==> // EH=HE+2E
==> // EF=FE-H
|
See
oppose;
opposite.
|









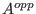 , where
, where 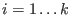 is the
opposite algebra of
is the
opposite algebra of 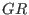 .
.