| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
7.9.2 Monomial orderings on free algebras
We provide many types of orderings for non-commutative Groebner bases up to a degree (length) bound. In general it is not clear, whether a given generating set has a finite Groebner bases with respect to some ordering.
Let
![]() = {
= {
![]() ,...,
,...,
![]() } be a set of symbols. A total ordering < on the free monoid
} be a set of symbols. A total ordering < on the free monoid
![]() with
with
![]() as the neutral element is called a monomial ordering if
as the neutral element is called a monomial ordering if
- it is a well-ordering, i.e., every non empty subset has a least element with respect to <, and
- it is compatible with multiplication, that is
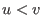 implies
implies
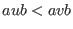 for all
for all
 ,
,
 ,
,
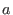 and
and
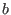 in
in
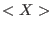 .
.
The left lexicographical ordering on
![]() with
with
![]() ...
...
![]() is defined as follows:
For arbitrary
is defined as follows:
For arbitrary
![]() ,
,
![]() in
in
![]() we say that
we say that
![]() , if
, if
-
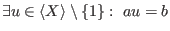 or
or -
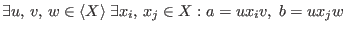 and
and 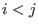 holds.
holds.
Note: left lex is not a monomial ordering, though it is a natural choice to break ties after, say, comparing elements by the total degree.
In a similar manner one can define the right lexicographical ordering.
On the monoid
![]() define the weight homomorphism
define the weight homomorphism
![]() , uniquely determined by
, uniquely determined by
![]() in
in
![]() for
for
![]() .
.
As a special case, define the length
len:
![]() by
by
![]() for
for
![]() .
.
For any ordering << on
![]() and any weight
and any weight
![]() define an ordering
define an ordering
![]() , called the
, called the
![]() -weight extension of
-weight extension of
![]() as follows:
For arbitrary
as follows:
For arbitrary
![]() ,
,
![]() in
in
![]() we say that
we say that
![]() if
if
-
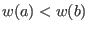 or
or
-
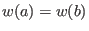 and
and
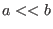 holds.
holds.
In a ring declaration, LETTERPLACE supports the following monomial orderings.
We illustrate each of the available choices by an example on the free monoid
![]() ,
,
![]() ,
,
![]() ,
where we order the monomials
,
where we order the monomials
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() correspondingly.
correspondingly.
- `
dp' - The degree right lexicographical ordering is the length-weight extension of the right lexicographical ordering.
With respect to the ordering `dp', the test monomials are ordered as follows:
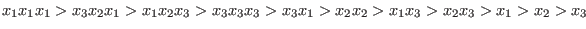
- `
Dp' - The degree left lexicographical ordering is the length-weight extension of the left lexicographical ordering.
With respect to the ordering `Dp', the test monomials are ordered as follows:
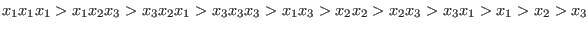
- `
Wp(w)for intvec w' - The weighted degree left lexicographical ordering is the
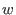 -weight extension of the left lexicographical ordering with weight
-weight extension of the left lexicographical ordering with weight
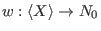 uniquely determined by strict positive
uniquely determined by strict positive
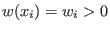 .
.
With respect to the ordering `Wp(1, 2, 1)', the test monomials are ordered as follows:
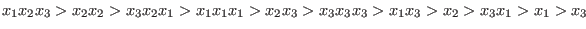
- `
lp' - Let
 be weights uniquely determined by
be weights uniquely determined by
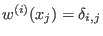 for
for
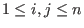 where
where 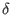 denotes the Kronecker delta. Let
denotes the Kronecker delta. Let 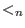 be the
be the 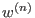 -weight extension of the left lexicographical ordering on
-weight extension of the left lexicographical ordering on
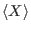 and inductively
and inductively 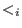 be the
be the 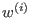 -weight extension of
-weight extension of 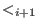 for all
for all 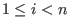 .
The monomial ordering lp corresponds to
.
The monomial ordering lp corresponds to 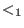 and eliminates
and eliminates 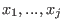 for all
for all 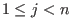 .
We refer to it as to left elimination ordering.
.
We refer to it as to left elimination ordering.The monomial ordering `lp' corresponds to
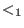 and eliminates {
and eliminates {
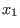 ,...,
,...,
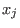 } for all
} for all
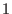 <=
<=
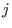 <
<
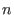 .
We refer to it as to left elimination ordering.
.
We refer to it as to left elimination ordering.
With respect to the ordering `lp', the test monomials are ordered as follows:
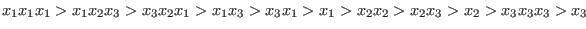
- `
rp' - Let
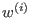 be weights uniquely determined by
be weights uniquely determined by
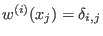 for
for
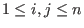 where
where 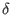 denotes the Kronecker delta. Let
denotes the Kronecker delta. Let 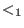 be the
be the 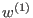 -weight extension of the left lexicographical ordering on
-weight extension of the left lexicographical ordering on
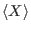 and inductively
and inductively 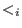 be the
be the 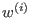 -weight extension of
-weight extension of 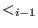 for all
for all 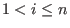 .
The monomial ordering rp corresponds to
.
The monomial ordering rp corresponds to 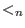 and eliminates
and eliminates
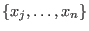 for all
for all 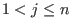 .
We refer to it as to right elimination ordering.
.
We refer to it as to right elimination ordering.The monomial ordering `rp' corresponds to
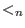 and eliminates {
and eliminates {
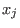 ,...,
,...,
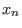 } for all
} for all
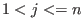 . We refer to it as to right elimination ordering.
. We refer to it as to right elimination ordering.
With respect to the ordering `rp', the test monomials are ordered as follows:
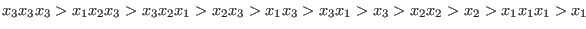
- `
(a(v), ordering)for intvec v' - For weight
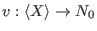 determined by
determined by
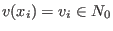 with
with 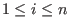 and monomial ordering
and monomial ordering 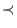 on
on
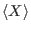 , the
, the 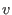 -weight extension of
-weight extension of 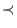 corresponds to (a(v), o). As a choice for
corresponds to (a(v), o). As a choice for 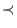 there are currently two options implemented, which are dp and Dp. Notice that this ordering eliminates
there are currently two options implemented, which are dp and Dp. Notice that this ordering eliminates
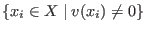 .
.With respect to the ordering `( a(1, 0, 0), Dp)', the test monomials are ordered as follows:
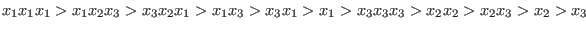
With ordering `( a(1, 1, 0), Dp)' one obtains:
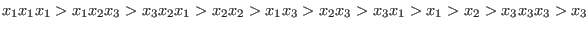
The examples are generated by the following code but with customized orderings denoted above.
LIB "freegb.lib"; ring r = 0, (x1,x2,x3),Dp; // variate ordering here ring R = freeAlgebra(r, 4); poly wr = x1*x1*x1+x3*x3*x3+x1*x2*x3+x3*x2*x1+x2*x2+x2*x3+x1*x3+x3*x1+x1+x2+x3; wr; // polynomial will be automatically ordered according to the ordering on R ==> x1*x1*x1+x1*x2*x3+x3*x2*x1+x3*x3*x3+x1*x3+x2*x2+x2*x3+x3*x1+x1+x2+x3 |