| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
5.1.12 coeffs
Syntax:coeffs (poly_expression,ring_variable)coeffs (ideal_expression,ring_variable)coeffs (vector_expression,ring_variable)coeffs (module_expression,ring_variable)coeffs (poly_expression,ring_variable,matrix_name)coeffs (ideal_expression,ring_variable,matrix_name)coeffs (vector_expression,ring_variable,matrix_name)coeffs (module_expression,ring_variable,matrix_name)Type:- matrix
Purpose:- develops each polynomial of the first argument J
as a univariate polynomial in the given ring_variable
z, and returns the coefficients as a matrix M.
With e denoting the maximal z-degree occuring in the polynomials of J, and d:=e+1, M =
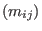 satisfies the following conditions:
satisfies the following conditions:
-
(i) If J is a single polynomial f, then M is a
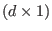 -matrix and
-matrix and
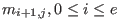 ,is the coefficient of
,is the coefficient of
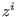 in f.
in f.
-
(ii) If J is an ideal with generators
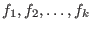 then M is a
then M is a
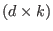 -matrix and
-matrix and
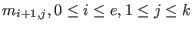 ,is the coefficient of
,is the coefficient of
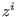 in
in
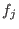 .
. -
(iii) If J is a k-dimensional vector with entries
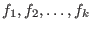 then M is a
then M is a
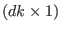 -matrix and
-matrix and
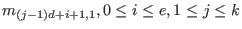 ,is the coefficient of
,is the coefficient of
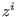 in
in
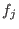 .
. -
(iV) If J is a module generated by s vectors
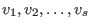 of dimension k then M is a
of dimension k then M is a
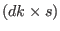 -matrix and
-matrix and
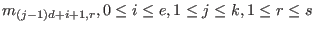 ,is the coefficient of
,is the coefficient of
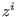 in the j-th entry of
in the j-th entry of
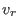 .
.
-
(i) If J is a single polynomial f, then M is a
Note:coeffsreturns the coefficient 0 at the appropriate matrix entry if a monomial is not present, whilecoefconsiders only monomials which actually occur in the given expression.Example:ring r; poly f = (x+y)^3; poly g = xyz+z10y4; ideal i = f, g; matrix M = coeffs(i, y); print(M); ==> x3, 0, ==> 3x2,xz, ==> 3x, 0, ==> 1, 0, ==> 0, z10 vector v = [f, g]; M = coeffs(v, y); print(M); ==> x3, ==> 3x2, ==> 3x, ==> 1, ==> 0, ==> 0, ==> xz, ==> 0, ==> 0, ==> z10
Syntax:coeffs (ideal_expression,ideal_expression)coeffs (module_expression,module_expression)coeffs (ideal_expression,ideal_expression,product_of_ringvars)coeffs (module_expression,module_expression,product_of_ringvars)Type:- matrix
Purpose:- expresses each polynomial of the first argument M as a sum
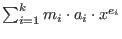 ,where the
,where the
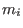 come from a specified set of monomials, the
come from a specified set of monomials, the
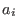 are from the underlying
coefficient ring (or field), and the
are from the underlying
coefficient ring (or field), and the
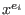 are powers of a specified ring variable x.
are powers of a specified ring variable x.
The second parameter K provides the set of monomials which should be sufficient to generate all entries of M.
Both M and K can be thought of as the matrices obtained by matrix(M) and matrix(K), respectively. (If M and K are given by ideals, then this matrix has just one row.)The optional parameter product_of_ringvars determines the variable x: It is expected to be either the product of all ring variables (then x is 1, and each polynomial will be expressed as
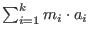 ,or product_of_ringvars is the product of all ring variables except one variable (which then determines x).
If product_of_ringvars is omitted then x = 1 as default.
,or product_of_ringvars is the product of all ring variables except one variable (which then determines x).
If product_of_ringvars is omitted then x = 1 as default.
If K contains all monomials that are necessary to express the entries of M, then the returned matrix A satisfies
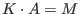 .Otherwise only a subset of entries of
.Otherwise only a subset of entries of
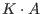 and M will coincide.
In this case, the valid entries start at M[1,1] and run from left to right, top to bottom.
and M will coincide.
In this case, the valid entries start at M[1,1] and run from left to right, top to bottom.
Note:- Note that in general not all entries of K*A and M will coincide, depending on the set of monomials
provided by K.
Example:ring r=32003,(x,y,z),dp; module M = [y3+x2z, xy], [-xy, y2+x2z]; print(M); ==> y3+x2z,-xy, ==> xy, x2z+y2 module K = [x2, xy], [y3, xy], [xy, x]; print(K); ==> x2,y3,xy, ==> xy,xy,x matrix A = coeffs(M, K, xy); // leaving z as variable of interest print(A); // attention: only the first row of M is reproduced by K*A ==> z,0, ==> 1,0, ==> 0,-1