| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
5.1.141 sres
Syntax:sres (ideal_expression,int_expression)sres (module_expression,int_expression)Type:- resolution
Purpose:- computes a free resolution of an ideal or module with Schreyer's
method. The ideal, resp. module, has to be a standard basis.
More precisely, let M be given by a standard basis and
 .Then
.Then srescomputes a free resolution of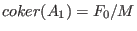
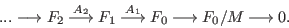
If the int expression k is not zero then the computation stops after k steps and returns a list of modules (given by standard bases) , i=1..k.
, i=1..k.sres(M,0)returns a list of n modules where n is the number of variables of the basering.Even if
sresdoes not compute a minimal resolution, thebetticommand gives the true betti numbers! In many cases of interestsresis much faster than any other known method. Letlist L=sres(M,0);thenL[1]=Mis identical to the input,L[2]is a standard basis with respect to the Schreyer ordering of the first syzygy module ofL[1], etc. (![${\tt L[i]}=M_i$](sing_135.png) in the notations from above.)
in the notations from above.)
Note:- Accessing single elements of a resolution may require some partial computations to be finished and may therefore take some time.
Example:ring r=31991,(t,x,y,z,w),ls; ideal M=t2x2+tx2y+x2yz,t2y2+ty2z+y2zw, t2z2+tz2w+xz2w,t2w2+txw2+xyw2; M=std(M); resolution L=sres(M,0); L; ==> 1 35 141 209 141 43 4 ==> r <-- r <-- r <-- r <-- r <-- r <-- r ==> ==> 0 1 2 3 4 5 6 ==> resolution not minimized yet ==> print(betti(L),"betti"); ==> 0 1 2 3 4 5 ==> ------------------------------------------ ==> 0: 1 - - - - - ==> 1: - - - - - - ==> 2: - - - - - - ==> 3: - 4 - - - - ==> 4: - - - - - - ==> 5: - - - - - - ==> 6: - - 6 - - - ==> 7: - - 9 16 2 - ==> 8: - - - 2 5 1 ==> ------------------------------------------ ==> total: 1 4 15 18 7 1 ==>