|
|
D.10.1.7 AGcode_Omega
Procedure from library brnoeth.lib (see brnoeth_lib).
- Usage:
- AGcode_Omega( G, D, EC ); G,D intvec, EC a list
- Return:
- a generator matrix for the residual AG code defined by the
divisors G and D.
- Note:
- The procedure must be called within the ring EC[1][4],
where EC is the output of
extcurve(d) (or within
the ring EC[1][2] if d=1).
The entry i in the intvec D refers to the i-th rational
place in EC[1][5] (i.e., to POINTS[i], etc., see extcurve).
The intvec G represents a rational divisor (see BrillNoether
for more details).
The code computes the residues of a vector space basis of
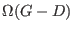 at the rational places given by D. at the rational places given by D.
- Warnings:
- G should satisfy
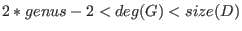 , which is
not checked by the algorithm. , which is
not checked by the algorithm.
G and D should have disjoint supports (checked by the algorithm).
Example:
| | LIB "brnoeth.lib";
int plevel=printlevel;
printlevel=-1;
ring s=2,(x,y),lp;
list HC=Adj_div(x3+y2+y);
==> The genus of the curve is 1
HC=NSplaces(1..2,HC);
HC=extcurve(2,HC);
==> Total number of rational places : NrRatPl = 9
def ER=HC[1][4];
setring ER;
intvec G=5; // the rational divisor G = 5*HC[3][1]
intvec D=2..9; // D = sum of the rational places no. 2..9 over F_4
// let us construct the corresponding residual AG code :
matrix C=AGcode_Omega(G,D,HC);
==> Vector basis successfully computed
// here is a linear code of type [8,3,>=5] over F_4
print(C);
==> (a+1),(a+1),1,(a), (a),1,0,0,
==> (a+1),(a), 1,0, 1, 0,1,0,
==> 1, 0, 1,(a+1),(a),0,0,1
printlevel=plevel;
|
See also:
AGcode_L;
Adj_div;
BrillNoether;
extcurve.
|