|
|
A.1.3 Rings associated to monomial orderings
In SINGULAR we may implement localizations of the polynomial ring
by choosing an appropriate monomial ordering (when defining the ring by
the ring command). We refer to Monomial orderings for a
thorough discussion of the monomial orderings available in
SINGULAR.
At this point, we restrict ourselves to describing the relation between
a monomial ordering and the ring (as mathematical object) which is
implemented by the ordering. This is most easily done by describing the
set of units: if > is a monomial ordering then precisely those elements
which have leading monomial 1 are considered as units (in all
computations performed with respect to this ordering).
In mathematical terms: choosing a monomial ordering > implements the
localization of the polynomial ring with respect to the multiplicatively
closed set of polynomials with leading monomial 1.
That is, choosing 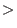 implements the ring implements the ring
If > is global (that is, 1 is the smallest monomial), the implemented
ring is just the polynomial ring. If > is local (that is, if 1 is the
largest monomial), the implemented ring is the localization of the
polynomial ring w.r.t. the homogeneous maximal ideal. For a mixed
ordering, we obtain "something in between these two rings":
| | ring R = 0,(x,y,z),dp; // polynomial ring (global ordering)
poly f = y4z3+2x2y2z2+4z4+5y2+1;
f; // display f in a degrevlex-ordered way
==> y4z3+2x2y2z2+4z4+5y2+1
short=0; // avoid short notation
f;
==> y^4*z^3+2*x^2*y^2*z^2+4*z^4+5*y^2+1
short=1;
leadmonom(f); // leading monomial
==> y4z3
ring r = 0,(x,y,z),ds; // local ring (local ordering)
poly f = fetch(R,f);
f; // terms of f sorted by degree
==> 1+5y2+4z4+2x2y2z2+y4z3
leadmonom(f); // leading monomial
==> 1
// Now we implement more "advanced" examples of rings:
//
// 1) (K[y]_<y>)[x]
//
int n,m=2,3;
ring A1 = 0,(x(1..n),y(1..m)),(dp(n),ds(m));
poly f = x(1)*x(2)^2+1+y(1)^10+x(1)*y(2)^5+y(3);
leadmonom(f);
==> x(1)*x(2)^2
leadmonom(1+y(1)); // unit
==> 1
leadmonom(1+x(1)); // no unit
==> x(1)
//
// 2) some ring in between (K[x]_<x>)[y] and K[x,y]_<x>
//
ring A2 = 0,(x(1..n),y(1..m)),(ds(n),dp(m));
leadmonom(1+x(1)); // unit
==> 1
leadmonom(1+x(1)*y(1)); // unit
==> 1
leadmonom(1+y(1)); // no unit
==> y(1)
//
// 3) K[x,y]_<x>
//
ring A4 = (0,y(1..m)),(x(1..n)),ds;
leadmonom(1+y(1)); // in ground field
==> 1
leadmonom(1+x(1)*y(1)); // unit
==> 1
leadmonom(1+x(1)); // unit
==> 1
|
Note, that even if we implictly compute over the localization of
the polynomial ring, most computations are explicitly performed with
polynomial data only.
In particular, 1/(1-x); does not return a power series
expansion or a fraction but 0 (division with remainder in polynomial ring).
See division for division with remainder in the localization and
invunit for a procedure returning a truncated power series expansion
of the inverse of a unit.
|
 Online Manual
Online Manual