|
|
B.2.6 Matrix orderings
Let
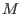 be an invertible be an invertible
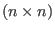 -matrix with integer coefficients and -matrix with integer coefficients and
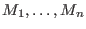 the rows of the rows of 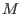 . .
The M-ordering < is defined as follows:
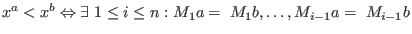 and and
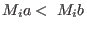 . .
Thus,
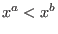 if and only if
if and only if 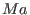 is smaller than is smaller than 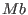 with respect to the lexicographical ordering. with respect to the lexicographical ordering.
The following matrices represent (for 3 variables) the global and
local orderings defined above (note that the matrix is not uniquely determined
by the ordering):
 lp: lp:
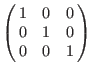 dp:
dp:
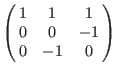 Dp:
Dp:

 wp(1,2,3): wp(1,2,3):
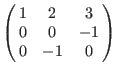 Wp(1,2,3):
Wp(1,2,3):
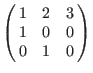
 ls: ls:
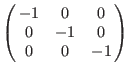 ds:
ds:
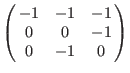 Ds:
Ds:
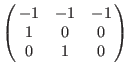
 ws(1,2,3): ws(1,2,3):
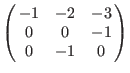 Ws(1,2,3):
Ws(1,2,3):
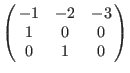
Product orderings (see next section) represented by a matrix:
 (dp(3), wp(1,2,3)): (dp(3), wp(1,2,3)):
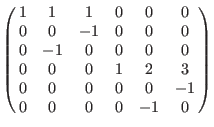
 (Dp(3), ds(3)): (Dp(3), ds(3)):
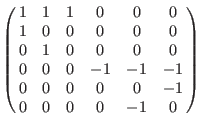
Orderings with extra weight vector (see below) represented by a matrix:
 (dp(3), a(1,2,3),dp(3)): (dp(3), a(1,2,3),dp(3)):
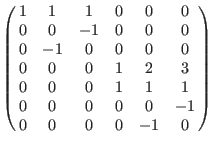
 (a(1,2,3,4,5),Dp(3), ds(3)): (a(1,2,3,4,5),Dp(3), ds(3)):
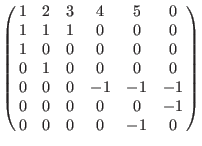
Example:
| | ring r = 0, (x,y,z), M(1, 0, 0, 0, 1, 0, 0, 0, 1);
|
which may also be written as:
| | intmat m[3][3]=1, 0, 0, 0, 1, 0, 0, 0, 1;
m;
==> 1,0,0,
==> 0,1,0,
==> 0,0,1
ring r = 0, (x,y,z), M(m);
r;
==> // coefficients: QQ
==> // number of vars : 3
==> // block 1 : ordering M
==> // : names x y z
==> // : weights 1 0 0
==> // : weights 0 1 0
==> // : weights 0 0 1
==> // block 2 : ordering C
|
If the ring has
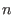 variables and the matrix does not contain variables and the matrix does not contain
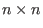 entries, an error message is given. entries, an error message is given.
WARNING: SINGULAR
does not check whether the matrix has full rank. In such a case some
computations might not terminate, others may not give a sensible result.
Having these matrix orderings SINGULAR can compute standard bases for
any monomial ordering which is compatible with the natural semigroup structure.
In practice the global and local orderings together with block orderings should be
sufficient in most cases. These orderings are faster than the corresponding
matrix orderings, since evaluating a matrix product is time consuming.
|