C.8.3 Generalized Newton identities
The error-locator polynomial is defined by
If this product is expanded,
then the coefficients 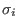 are the elementary symmetric functions in
the error locations are the elementary symmetric functions in
the error locations 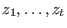
Generalized Newton identities
The syndromes
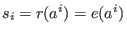 and the coefficients and the coefficients 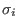 satisfy
the following generalized Newton identities: satisfy
the following generalized Newton identities:
Decoding up to error-correcting capacity
We have
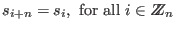 , since , since
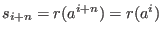 . Furthermore . Furthermore
and
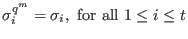 .
Replace the syndromes by variables and obtain the following set of polynomials .
Replace the syndromes by variables and obtain the following set of polynomials  in the variables in the variables
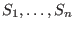 and and
 : :
For an example see sysNewton in decodegb_lib. More on this method and the method based on
Waring function can be found in [ABF2002]. See also [ABF2008].
|
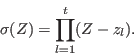
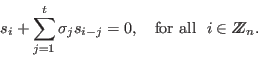
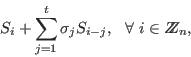
 Online Manual
Online Manual