| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
4.11 map
Maps are ring maps from a preimage ring into the basering.
Note:
- The target of a map is ALWAYS the actual basering
- The preimage ring has to be stored "by its name", that means, maps can only be used in such contexts, where the name of the preimage ring can be resolved (this has to be considered in subprocedures). See also Identifier resolution, Names in procedures.
Maps between rings with different coefficient fields are possible and listed below.
Canonically realized are
-
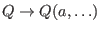 (
(
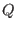 : the rational numbers)
: the rational numbers)
-
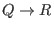 (
(
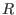 : the real numbers)
: the real numbers)
-
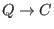 (
(
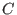 : the complex numbers)
: the complex numbers)
-
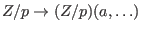 (
(
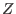 : the integers)
: the integers)
-
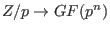 (
(
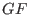 : the Galois field)
: the Galois field)
-
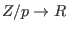
-
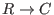
Possible are furthermore
-
![$Z/p \rightarrow Q,
\quad
[i]_p \mapsto i \in [-p/2, \, p/2]
\subseteq Z$](sing_84.png)
-
![$Z/p \rightarrow Z/p^\prime,
\quad
[i]_p \mapsto i \in [-p/2, \, p/2] \subseteq Z, \;
i \mapsto [i]_{p^\prime} \in Z/p^\prime$](sing_85.png)
-
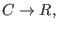 by taking the real part
by taking the real part
Finally, in SINGULAR we allow the mapping from rings with coefficient field Q to rings whose ground fields have finite characteristic:
4.11.1 map declarations 4.11.2 map expressions 4.11.3 map operations 4.11.4 map related functions