| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
A.3.3 Elimination
Elimination is the algebraic counterpart of the geometric concept of
projection. If
![]() is a polynomial map,
the Zariski-closure of the image is the zero-set of the ideal
is a polynomial map,
the Zariski-closure of the image is the zero-set of the ideal
![]() ,where
,where
that is, of the ideal j obtained from J by eliminating the variables
Since elimination is expensive, it may be useful to use a Hilbert-driven approach to the elimination problem (see Groebner basis conversion):
First compute the Hilbert function of the ideal w.r.t.
a fast ordering (e.g., dp), then make use of it to speed up the
computation by a Hilbert-driven elimination which uses the intvec provided as
third argument.
In SINGULAR the most convenient way is to use the
eliminate command.
In contrast to the first method, with eliminate the result needs not be a
standard basis in the given ordering.
Hence, there may be cases where the first method is the preferred one.
WARNING: In the case of a local or a mixed ordering,
elimination needs special care. f may be considered as a map of germs
![]() ,but even
if this map germ is finite, we are in general not able to compute the image
germ because for this we would need an implementation of the Weierstrass
preparation theorem. What we can compute, and what
,but even
if this map germ is finite, we are in general not able to compute the image
germ because for this we would need an implementation of the Weierstrass
preparation theorem. What we can compute, and what eliminate
actually does, is the following: let V(J) be the zero-set of J in
![]() ,then the
closure of the image of V(J) under the projection
,then the
closure of the image of V(J) under the projection
can be computed.(Note that this germ contains also those components of V(J) which meet the fiber of pr outside the origin.) This is achieved by an ordering with the block of t-variables having a global ordering (and preceding the x-variables) and the x-variables having a local ordering.
In any case, if the input is weighted homogeneous (=quasihomogeneous),
the weights given to the variables should be chosen accordingly.
SINGULAR offers a function weight which proposes,
given an ideal or module, integer weights for the variables, such that
the ideal, resp. module, is as homogeneous as possible with respect to these weights.
The function finds correct weights, if the input is weighted homogeneous
(but is rather slow for many variables). In order to check, whether the
input is quasihomogeneous, use the function qhweight, which returns
an intvec of correct weights if the input is quasihomogeneous and an intvec
of zeros otherwise.
Let us give three examples:
- First we compute the equations of the simple space curve 'T[7]' consisting of two tangential cusps given in parametric form.
- We compute weights for the equations such that the equations are quasihomogeneous w.r.t. these weights.
-
Then we compute the tangent developable of the rational
normal curve in
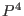 .
.
// 1. Compute equations of curve given in parametric form:
// Two transversal cusps in (k^3,0):
ring r1 = 0,(t,x,y,z),ls;
ideal i1 = x-t2,y-t3,z; // parametrization of the first branch
ideal i2 = y-t2,z-t3,x; // parametrization of the second branch
ideal j1 = eliminate(i1,t);
j1; // equations of the first branch
==> j1[1]=z
==> j1[2]=y2-x3
ideal j2 = eliminate(i2,t);
j2; // equations of the second branch
==> j2[1]=z2-y3
==> j2[2]=x
// Now map to a ring with only x,y,z as variables and compute the
// intersection of j1 and j2 there:
ring r2 = 0,(x,y,z),ds;
ideal j1= imap(r1,j1); // imap is a convenient ringmap for
ideal j2= imap(r1,j2); // inclusions and projections of rings
ideal i = intersect(j1,j2);
i; // equations of both branches
==> i[1]=z2-y3+x3y
==> i[2]=xz
==> i[3]=xy2-x4
//
// 2. Compute the weights:
intvec v= qhweight(i); // compute weights
v;
==> 4,6,9
//
// 3. Compute the tangent developable
// The tangent developable of a projective variety given parametrically
// by F=(f1,...,fn) : P^r --> P^n is the union of all tangent spaces
// of the image. The tangent space at a smooth point F(t1,...,tr)
// is given as the image of the tangent space at (t1,...,tr) under
// the tangent map (affine coordinates)
// T(t1,...,tr): (y1,...,yr) --> jacob(f)*transpose((y1,...,yr))
// where jacob(f) denotes the jacobian matrix of f with respect to the
// t's evaluated at the point (t1,...,tr).
// Hence we have to create the graph of this map and then to eliminate
// the t's and y's.
// The rational normal curve in P^4 is given as the image of
// F(s,t) = (s4,s3t,s2t2,st3,t4)
// each component being homogeneous of degree 4.
ring P = 0,(s,t,x,y,a,b,c,d,e),dp;
ideal M = maxideal(1);
ideal F = M[1..2]; // take the 1st two generators of M
F=F^4;
// simplify(...,2); deletes 0-columns
matrix jac = simplify(jacob(F),2);
ideal T = x,y;
ideal J = jac*transpose(T);
ideal H = M[5..9];
ideal i = matrix(H)-matrix(J);// this is tricky: difference between two
// ideals is not defined, but between two
// matrices. By type conversion
// the ideals are converted to matrices,
// subtracted and afterwards converted
// to an ideal. Note that '+' is defined
// and adds (concatenates) two ideals
i;
==> i[1]=-4s3x+a
==> i[2]=-3s2tx-s3y+b
==> i[3]=-2st2x-2s2ty+c
==> i[4]=-t3x-3st2y+d
==> i[5]=-4t3y+e
// Now we define a ring with product ordering and weights 4
// for the variables a,...,e.
// Then we map i from P to P1 and eliminate s,t,x,y from i.
ring P1 = 0,(s,t,x,y,a,b,c,d,e),(dp(4),wp(4,4,4,4,4));
ideal i = fetch(P,i);
ideal j= eliminate(i,stxy); // equations of tangent developable
j;
==> j[1]=3c2-4bd+ae
==> j[2]=2bcd-3ad2-3b2e+4ace
==> j[3]=8b2d2-9acd2-9b2ce+14abde-4a2e2
// We can use the product ordering to eliminate s,t,x,y from i
// by a std-basis computation.
// We need proc 'nselect' from elim.lib.
LIB "elim.lib";
j = std(i); // compute a std basis j
j = nselect(j,1..4); // select generators from j not
j; // containing variable 1,...,4
==> j[1]=3c2-4bd+ae
==> j[2]=2bcd-3ad2-3b2e+4ace
==> j[3]=8b2d2-9acd2-9b2ce+12ac2e-2abde
|