| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
A.3.6 Computation of Ext
We start by showing how to calculate the n-th Ext group of an ideal. The ingredients to do this are by the definition of Ext the following: calculate a (minimal) resolution at least up to length n, apply the Hom functor, and calculate the n-th homology group, that is, form the quotient ker/im in the resolution sequence.
The Hom functor is given simply by transposing (hence dualizing) the
module or the corresponding matrix with the command transpose.
The image of the (n-1)-st map is generated by the columns of the
corresponding matrix. To calculate the kernel apply the command
syz at the (n-1)-st transposed entry of the resolution.
Finally, the quotient is obtained by the command modulo, which
gives for two modules A = ker, B = Im the module of relations of
in the usual way. As we have a chain complex, this is obviously the same as ker/Im.
We collect these statements in the following short procedure:
proc ext(int n, ideal I)
{
resolution rs = mres(I,n+1);
module tAn = transpose(rs[n+1]);
module tAn_1 = transpose(rs[n]);
module ext_n = modulo(syz(tAn),tAn_1);
return(ext_n);
}
|
Now consider the following example:
ring r5 = 32003,(a,b,c,d,e),dp; ideal I = a2b2+ab2c+b2cd, a2c2+ac2d+c2de,a2d2+ad2e+bd2e,a2e2+abe2+bce2; print(ext(2,I)); ==> 1,0,0,0,0,0,0, ==> 0,1,0,0,0,0,0, ==> 0,0,1,0,0,0,0, ==> 0,0,0,1,0,0,0, ==> 0,0,0,0,1,0,0, ==> 0,0,0,0,0,1,0, ==> 0,0,0,0,0,0,1 ext(3,I); // too big to be displayed here |
The library homolog.lib contains several procedures for computing
Ext-modules and related modules, which are much more general and
sophisticated than the above one. They are used in the following
example:
If
![]() is a module, then
is a module, then
![]() , resp.
, resp.
![]() ,are the modules of infinitesimal deformations, respectively of obstructions,
of
,are the modules of infinitesimal deformations, respectively of obstructions,
of
![]() (like T1 and T2 for a singularity). Similar to the treatment of
singularities, the semiuniversal deformation of
(like T1 and T2 for a singularity). Similar to the treatment of
singularities, the semiuniversal deformation of
![]() can be computed (if
can be computed (if
![]() is finite dimensional) with the help of
is finite dimensional) with the help of
![]() ,
, ![]() and the cup product.
There is an extra procedure for
and the cup product.
There is an extra procedure for
![]() if
if
![]() is an ideal in
is an ideal in
![]() , since this is faster than the
general Ext.
, since this is faster than the
general Ext.
We compute
-
the infinitesimal deformations
(
 )and obstructions
(
)and obstructions
(
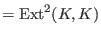 )of the residue field
)of the residue field
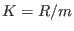 of an ordinary cusp,
of an ordinary cusp,
![$R=K[x,y]_m/(x^2-y^3)$](sing_466.png) ,
, 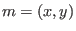 .To compute
.To compute
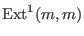 we have to apply
we have to apply Ext(1,syz(m),syz(m))withsyz(m)the first syzygy module of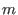 , which is isomorphic to
, which is isomorphic to
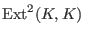 .
. -
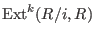 for some ideal
for some ideal
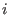 and with an extra option.
and with an extra option.
LIB "homolog.lib"; ring R=0,(x,y),ds; ideal i=x2-y3; qring q = std(i); // defines the quotient ring k[x,y]_m/(x2-y3) ideal m = maxideal(1); module T1K = Ext(1,m,m); // computes Ext^1(R/m,R/m) ==> // dimension of Ext^1: 0 ==> // vdim of Ext^1: 2 ==> print(T1K); ==> 0,x,0,y, ==> x,0,y,0 printlevel=2; // gives more explanation module T2K=Ext(2,m,m); // computes Ext^2(R/m,R/m) ==> // Computing Ext^2 (help Ext; gives an explanation): ==> // Let 0<--coker(M)<--F0<--F1<--F2<--... be a resolution of coker(M), ==> // and 0<--coker(N)<--G0<--G1 a presentation of coker(N), ==> // then Hom(F2,G0)-->Hom(F3,G0) is given by: ==> y2,x, ==> x, y ==> // and Hom(F1,G0) + Hom(F2,G1)-->Hom(F2,G0) is given by: ==> -y,x, x,0,y,0, ==> x, -y2,0,x,0,y ==> ==> // dimension of Ext^2: 0 ==> // vdim of Ext^2: 2 ==> print(std(T2K)); ==> 0,x,0,y, ==> x,0,y,0 printlevel=0; module E = Ext(1,syz(m),syz(m)); ==> // dimension of Ext^1: 0 ==> // vdim of Ext^1: 2 ==> print(std(E)); ==> 0,0,0,x,0,y, ==> 0,0,x,0,y,0, ==> 0,1,0,0,0,0, ==> 1,0,0,0,0,0 //The matrices which we have just computed are presentation matrices //of the modules T2K and E. Hence we may ignore those columns //containing 1 as an entry and see that T2K and E are isomorphic //as expected, but differently presented. //------------------------------------------- ring S=0,(x,y,z),dp; ideal i = x2y,y2z,z3x; module E = Ext_R(2,i); ==> // dimension of Ext^2: 1 ==> print(E); ==> 0,y,0,z2, ==> z,0,0,-x, ==> 0,0,x,-y // if a 3-rd argument of type int is given, // a list of Ext^k(R/i,R), a SB of Ext^k(R/i,R) and a vector space basis // is returned: list LE = Ext_R(3,i,0); ==> // dimension of Ext^3: 0 ==> // vdim of Ext^3: 2 ==> LE; ==> [1]: ==> _[1]=y*gen(1) ==> _[2]=x*gen(1) ==> _[3]=z2*gen(1) ==> [2]: ==> _[1]=y*gen(1) ==> _[2]=x*gen(1) ==> _[3]=z2*gen(1) ==> [3]: ==> _[1,1]=z ==> _[1,2]=1 print(LE[2]); ==> y,x,z2 print(kbase(LE[2])); ==> z,1 |