|
|
7.3.19 oppose
Syntax:
oppose ( ring_name, name )
Type:
- poly, vector, ideal, module or matrix (the same type as the second argument)
Purpose:
- for a given object in the given ring, creates its opposite object
in the opposite ( opposite) ring (the last one is assumed to be the current ring).
Remark:
- for any object
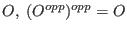 . .| | LIB "ncalg.lib";
def R = makeUsl2();
setring R;
matrix m[3][4];
poly p = (h^2-1)*f*e;
vector v = [1,e*h,0,p];
ideal i = h*e, f^2*e,h*f*e;
m = e,f,h,1,0,h^2, p,0,0,1,e^2,e*f*h+1;
module mm = module(m);
def b = opposite(R);
setring b; b;
==> // coefficients: QQ
==> // number of vars : 3
==> // block 1 : ordering a
==> // : names H F E
==> // : weights 1 1 1
==> // block 2 : ordering ls
==> // : names H F E
==> // block 3 : ordering C
==> // noncommutative relations:
==> // FH=HF-2F
==> // EH=HE+2E
==> // EF=FE-H
// we will oppose these objects: p,v,i,m,mm
poly P = oppose(R,p);
vector V = oppose(R,v);
ideal I = oppose(R,i);
matrix M = oppose(R,m);
module MM = oppose(R,mm);
def c = opposite(b);
setring c; // now let's check the correctness:
// print compact presentations of objects
print(oppose(b,P)-imap(R,p));
==> 0
print(oppose(b,V)-imap(R,v));
==> [0]
print(matrix(oppose(b,I))-imap(R,i));
==> 0,0,0
print(matrix(oppose(b,M))-imap(R,m));
==> 0,0,0,0,
==> 0,0,0,0,
==> 0,0,0,0
print(matrix(oppose(b,MM))-imap(R,mm));
==> 0,0,0,0,
==> 0,0,0,0,
==> 0,0,0,0
|
See
envelope;
opposite.
|









 .
.