|
|
D.4.25.11 finiteDiagInvariants
Procedure from library normaliz.lib (see normaliz_lib).
- Usage:
- finiteDiagInvariants(intmat U);
finiteDiagInvariants(intmat U, intvec grading);
- Return:
- This function computes the ring of invariants of a finite abelian group
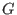 acting diagonally on the surrounding polynomial ring
acting diagonally on the surrounding polynomial ring
![$K[X_1,...,X_n]$](sing_1036.png) . The
group is the direct product of cyclic groups generated by finitely many
elements . The
group is the direct product of cyclic groups generated by finitely many
elements 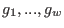 . The element . The element 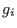 acts on the indeterminate acts on the indeterminate 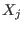 by by
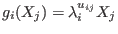 where where 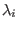 is a primitive root of
unity of order equal to is a primitive root of
unity of order equal to 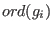 . The ring of invariants is generated by all
monomials satisfying the system . The ring of invariants is generated by all
monomials satisfying the system
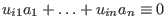 mod ord mod ord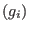 , , 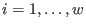 .
The input to the function is the .
The input to the function is the 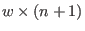 matrix matrix 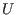 with rows with rows
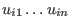 ord ord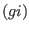 , , 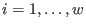 . The output is a monomial ideal
listing the algebra generators of the subalgebra of invariants . The output is a monomial ideal
listing the algebra generators of the subalgebra of invariants
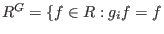 for all for all
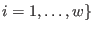 . .
The function returns the ideal given by the input matrix C if one of
the options supp, triang, volume, or
hseries has been activated.
However, in this case some numerical invariants are computed, and
some other data may be contained in files that you can read into
Singular (see showNuminvs, exportNuminvs).
- Note:
Example:
| | LIB "normaliz.lib";
ring R = 0,(x,y,z,w),dp;
intmat C[2][5] = 1,1,1,1,5, 1,0,2,0,7;
finiteDiagInvariants(C);
==> _[1]=w5
==> _[2]=z7w3
==> _[3]=z14w
==> _[4]=z35
==> _[5]=yw4
==> _[6]=yz7w2
==> _[7]=yz14
==> _[8]=y2w3
==> _[9]=y2z7w
==> _[10]=y3w2
==> _[11]=y3z7
==> _[12]=y4w
==> _[13]=y5
==> _[14]=xz3w
==> _[15]=xz24
==> _[16]=xyz3
==> _[17]=x2z13
==> _[18]=x3z2
==> _[19]=x5zw4
==> _[20]=x5yzw3
==> _[21]=x5y2zw2
==> _[22]=x5y3zw
==> _[23]=x5y4z
==> _[24]=x7w3
==> _[25]=x7yw2
==> _[26]=x7y2w
==> _[27]=x7y3
==> _[28]=x12zw2
==> _[29]=x12yzw
==> _[30]=x12y2z
==> _[31]=x14w
==> _[32]=x14y
==> _[33]=x19z
==> _[34]=x35
|
See also:
diagInvariants;
intersectionValRingIdeals;
intersectionValRings;
torusInvariants.
|









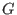 acting diagonally on the surrounding polynomial ring
acting diagonally on the surrounding polynomial ring
![$K[X_1,...,X_n]$](sing_1036.png) . The
group is the direct product of cyclic groups generated by finitely many
elements
. The
group is the direct product of cyclic groups generated by finitely many
elements 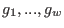 . The element
. The element 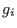 acts on the indeterminate
acts on the indeterminate 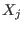 by
by
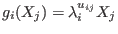 where
where 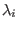 is a primitive root of
unity of order equal to
is a primitive root of
unity of order equal to 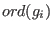 . The ring of invariants is generated by all
monomials satisfying the system
. The ring of invariants is generated by all
monomials satisfying the system
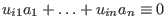 mod ord
mod ord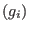 ,
, 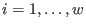 .
The input to the function is the
.
The input to the function is the 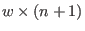 matrix
matrix 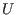 with rows
with rows
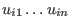 ord
ord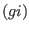 ,
, 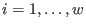 . The output is a monomial ideal
listing the algebra generators of the subalgebra of invariants
. The output is a monomial ideal
listing the algebra generators of the subalgebra of invariants
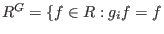 for all
for all
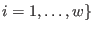 .
.