|
|
5.1.98 mres
Syntax:
mres ( ideal_expression, int_expression )
mres ( module_expression, int_expression )
Type:
- resolution
Purpose:
- computes a minimal free resolution of an ideal or module M with the
standard basis method. More precisely, let A=
matrix(M), then mres
computes a free resolution of
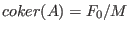
where the columns of the matrix
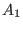 are a minimal set of generators
of M if the basering is local or if M is homogeneous.
If the int expression k is not zero, then the computation stops after k steps
and returns a list of modules are a minimal set of generators
of M if the basering is local or if M is homogeneous.
If the int expression k is not zero, then the computation stops after k steps
and returns a list of modules
 , i=1...k. , i=1...k.
mres(M,0) returns a resolution consisting of at most n+2 modules,
where n is the number of variables of the basering.
Let list L=mres(M,0);
then L[1] consists of a minimal set of generators of the input, L[2]
consists of a minimal set of generators for the first syzygy module of
L[1], etc., until L[p+1], such that
![${\tt L[i]}\neq 0$](sing_167.png) for for 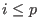 , but , but L[p+1], the first syzygy module of L[p],
is 0 (if the basering is not a qring).
Note:
- Accessing single elements of a resolution may require some partial
computations to be finished and may therefore take some time.
Note:
mres honours degBound.
Example:
| | ring r=31991,(t,x,y,z,w),ls;
ideal M=t2x2+tx2y+x2yz,t2y2+ty2z+y2zw,
t2z2+tz2w+xz2w,t2w2+txw2+xyw2;
resolution L=mres(M,0);
L;
==> 1 4 15 18 7 1
==> r <-- r <-- r <-- r <-- r <-- r
==>
==> 0 1 2 3 4 5
==>
// projective dimension of M is 5
|
See
degBound;
fres;
hres;
ideal;
lres;
module;
res;
sres.
|









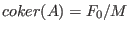
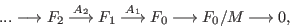
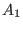 are a minimal set of generators
of M if the basering is local or if M is homogeneous.
If the int expression k is not zero, then the computation stops after k steps
and returns a list of modules
are a minimal set of generators
of M if the basering is local or if M is homogeneous.
If the int expression k is not zero, then the computation stops after k steps
and returns a list of modules
 , i=1...k.
, i=1...k.![${\tt L[i]}\neq 0$](sing_167.png) for
for 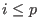 , but
, but