7.3.1 betti (plural)

Syntax:

betti ( list_expression )
betti ( resolution_expression )
betti ( list_expression , int_expression )
betti ( resolution_expression , int_expression )

Type:

intmat

Note:

in the non-commutative case, computing Betti numbers makes sense only if the basering 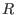has homogeneous relations. The output of the command can be pretty-printed using print( , "betti"), i.e., with "betti" as second argument; see below example.

Purpose:

with 1 argument: computes the graded Betti numbers of a minimal resolution o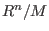f , if 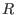denotes the basering and 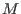a homogeneous submodule of 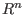and the argument represents a resolution of .
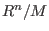The entry d of the intmat at place (i, j) is the minimal number of generators in degree i+j of the j-th syzygy module (= module of relations) of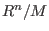 (the 0th (resp. 1st) syzygy module of 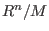is 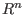(resp. 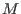)).The argument is considered to be the result of a mres or nres command. This implies that a zero is only allowed (and counted) as a generator in the first module.
For the computation betti uses only the initial monomials. This could lead to confusing results for a non-homogeneous input.

If the optional second argument is non-zero, the Betti numbers will be minimized.

Example:

int i;int N=2; ring r=0,(x(1..N),d(1..N),q(1..N)),Dp; matrix D[3*N][3*N]; for (i=1;i<=N;i++) { D[i,N+i]=q(i)^2; } def W=nc_algebra(1,D); setring W; // this algebra is a kind of homogenized Weyl algebra W; ==> // coefficients: QQ considered as a field ==> // number of vars : 6 ==> // block 1 : ordering Dp ==> // : names x(1) x(2) d(1) d(2) q(1) q(2) ==> // block 2 : ordering C ==> // noncommutative relations: ==> // d(1)x(1)=x(1)*d(1)+q(1)^2 ==> // d(2)x(2)=x(2)*d(2)+q(2)^2 ideal I = x(1),x(2),d(1),d(2),q(1),q(2); option(redSB); option(redTail); resolution R = mres(I,0); // thus R will be the full length minimal resolution print(betti(R),"betti"); ==> 0 1 2 3 4 5 6 ==> ------------------------------------------------ ==> 0: 1 6 15 20 15 6 1 ==> ------------------------------------------------ ==> total: 1 6 15 20 15 6 1 ==>