|
|
7.3.16 nc_algebra
Syntax:
nc_algebra( matrix_expression C, matrix_expression D )
nc_algebra( number_expression n, matrix_expression D )
nc_algebra( matrix_expression C, poly_expression p )
nc_algebra( number_expression n, poly_expression p )
Type:
- ring
Purpose:
- Executed in the basering
r, say, in k variables
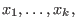 nc_algebra creates and returns the
non-commutative extension of r subject to relations
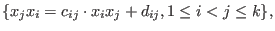 where
where 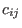 and and 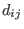 must be put into two strictly upper triangular matrices must be put into two strictly upper triangular matrices C with entries
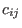 from the ground field of from the ground field of r
and D with (commutative) polynomial entries
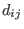 from from r. See all the details in G-algebras.
If
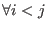 , , 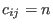 ,one can input the number ,one can input the number n instead of matrix C.
If
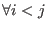 , , 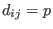 ,one can input the polynomial ,one can input the polynomial p instead of matrix D.
Note: The returned ring should be activated afterwards, using the command setring.
Note: The coefficients must be a field (see G-algebras).
Remark:
- At present, PLURAL does not check the non-degeneracy conditions (see G-algebras) while setting an algebra.
Example:
| | LIB "nctools.lib";
// ------- first example: C, D are matrices --------
ring r1 = (0,Q),(x,y,z),Dp;
minpoly = rootofUnity(6);
matrix C[3][3];
matrix D[3][3];
C[1,2]=Q2; C[1,3]=1/Q2; C[2,3]=Q2;
D[1,2]=-Q*z; D[1,3]=1/Q*y; D[2,3]=-Q*x;
def S=nc_algebra(C,D);
// this algebra is a quantum deformation U'_q(so_3),
// where Q is a 6th root of unity
setring S;S;
==> // coefficients: QQ[Q]/(Q2-Q+1) considered as a field
==> // number of vars : 3
==> // block 1 : ordering Dp
==> // : names x y z
==> // block 2 : ordering C
==> // noncommutative relations:
==> // yx=(Q-1)*xy+(-Q)*z
==> // zx=(-Q)*xz+(-Q+1)*y
==> // zy=(Q-1)*yz+(-Q)*x
kill r1,S;
// ----- second example: number n=1, D is a matrix
ring r2=0,(Xa,Xb,Xc,Ya,Yb,Yc,Ha,Hb),dp;
matrix d[8][8];
d[1,2]=-Xc; d[1,4]=-Ha; d[1,6]=Yb; d[1,7]=2*Xa;
d[1,8]=-Xa; d[2,5]=-Hb; d[2,6]=-Ya; d[2,7]=-Xb;
d[2,8]=2*Xb; d[3,4]=Xb; d[3,5]=-Xa; d[3,6]=-Ha-Hb;
d[3,7]=Xc; d[3,8]=Xc; d[4,5]=Yc; d[4,7]=-2*Ya;
d[4,8]=Ya; d[5,7]=Yb; d[5,8]=-2*Yb;
d[6,7]=-Yc; d[6,8]=-Yc;
def S=nc_algebra(1,d); // this algebra is U(sl_3)
setring S;S;
==> // coefficients: QQ considered as a field
==> // number of vars : 8
==> // block 1 : ordering dp
==> // : names Xa Xb Xc Ya Yb Yc Ha Hb
==> // block 2 : ordering C
==> // noncommutative relations:
==> // XbXa=Xa*Xb-Xc
==> // YaXa=Xa*Ya-Ha
==> // YcXa=Xa*Yc+Yb
==> // HaXa=Xa*Ha+2*Xa
==> // HbXa=Xa*Hb-Xa
==> // YbXb=Xb*Yb-Hb
==> // YcXb=Xb*Yc-Ya
==> // HaXb=Xb*Ha-Xb
==> // HbXb=Xb*Hb+2*Xb
==> // YaXc=Xc*Ya+Xb
==> // YbXc=Xc*Yb-Xa
==> // YcXc=Xc*Yc-Ha-Hb
==> // HaXc=Xc*Ha+Xc
==> // HbXc=Xc*Hb+Xc
==> // YbYa=Ya*Yb+Yc
==> // HaYa=Ya*Ha-2*Ya
==> // HbYa=Ya*Hb+Ya
==> // HaYb=Yb*Ha+Yb
==> // HbYb=Yb*Hb-2*Yb
==> // HaYc=Yc*Ha-Yc
==> // HbYc=Yc*Hb-Yc
kill r2,S;
// ---- third example: C is a matrix, p=0 is a poly
ring r3=0,(a,b,c,d),lp;
matrix c[4][4];
c[1,2]=1; c[1,3]=3; c[1,4]=-2;
c[2,3]=-1; c[2,4]=-3; c[3,4]=1;
def S=nc_algebra(c,0); // it is a quasi--commutative algebra
setring S;S;
==> // coefficients: QQ considered as a field
==> // number of vars : 4
==> // block 1 : ordering lp
==> // : names a b c d
==> // block 2 : ordering C
==> // noncommutative relations:
==> // ca=3ac
==> // da=-2ad
==> // cb=-bc
==> // db=-3bd
kill r3,S;
// -- fourth example : number n = -1, poly p = 3w
ring r4=0,(u,v,w),dp;
def S=nc_algebra(-1,3w);
setring S;S;
==> // coefficients: QQ considered as a field
==> // number of vars : 3
==> // block 1 : ordering dp
==> // : names u v w
==> // block 2 : ordering C
==> // noncommutative relations:
==> // vu=-uv+3w
==> // wu=-uw+3w
==> // wv=-vw+3w
kill r4,S;
|
See also
ncalg_lib;
nctools_lib;
qmatrix_lib.
|









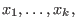
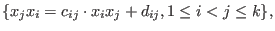 where
where 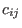 and
and 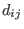 must be put into two strictly upper triangular matrices
must be put into two strictly upper triangular matrices 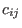 from the ground field of
from the ground field of 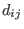 from
from 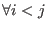 ,
, 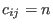 ,one can input the number
,one can input the number 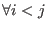 ,
, 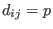 ,one can input the polynomial
,one can input the polynomial