| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
7.7 LETTERPLACE

A Subsystem for Non-commutative Finitely Presented Associative Algebras
This section describes mathematical notions and definitions used in the LETTERPLACE subsystem of SINGULAR.
All algebras are assumed to be associative
![]() -algebras for
-algebras for
![]() being a field
being a field
![]()
or a ring
![]() .
.
- What is and what does LETTERPLACE?
What is LETTERPLACE? It is a subsystem of SINGULAR, providing the manipulations and computations within free associative algebras over rings
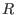
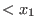 ,...,
,...,
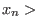 ,
where the coefficient domain
,
where the coefficient domain
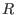 is either a ring
is either a ring
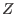 or
a field, supported by SINGULAR.
or
a field, supported by SINGULAR.
LETTERPLACE can perform computations also in the factor-algebras of the above (via data type
qring) by two-sided ideals.Free algebras are internally represented in SINGULAR as so-called Letterplace rings.
Each such ring is constructed from a commutative ring
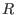 [
[
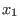 ,...,
,...,
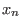 ]
and a degree (length) bound
]
and a degree (length) bound
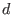 .
.
This encodes a sub-
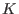 -vector space (also called a filtered part) of
-vector space (also called a filtered part) of
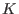
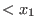 ,...,
,...,
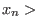 ,
spanned by all monomials of length at most
,
spanned by all monomials of length at most
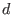 .
Analogously for free
.
Analogously for free
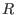 -subbimodules of a free
-subbimodules of a free
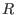 -bimodule of a fixed rank.
-bimodule of a fixed rank.
Within such a construction we offer the computations of Groebner (also known as Groebner-Shirshov) bases, normal forms, syzygies and many more.
We address both two-sided ideals and subbimodules of the free bimodule of the fixed rank.
A variety of monomial and module orderings is supported, including elimination orderings for both variables and bimodule components. A monomial ordering has to be a well-ordering.
LETTERPLACE works with every field, supported by SINGULAR, and with the coefficient ring
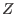 .
.
Note, that the elements of the coefficient field (or a ring) mutually commute with all variables.