A.2.2 Groebner basis conversion

The performance of Buchberger's algorithm is sensitive to the chosen monomial order. A Groebner basis computation with respect to a less favorable order such as the lexicographic ordering may easily run out of time or memory even in cases where a Groebner basis computation with respect to a more efficient order such as the degree reverse lexicographic ordering is very well feasible. Groebner basis conversion algorithms and the Hilbert-driven Buchberger algorithm are based on this observation:

• Groebner basis conversion: Given an ideal and a slow monomial order, compute a Groebner basis with respect to an appropriately chosen fast order. Then convert the result to a Groebner basis with respect to the given slow order.

• Hilbert-driven Buchberger algorithm: Homogenize the given generators for 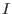with respect to a new variable, say, 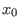. Extend the given slow ordering on to a global product ordering on . Compute a Groebner basis for the ideal generated by the homogenized polynomials with respect to a fast ordering. Read the Hilbert function, and use this information when computing a Groebner basis with respect to the extended (slow) ordering. Finally, dehomogenize the elements of the resulting Groebner basis.

SINGULAR provides implementations for the FGLM conversion algorithm (which applies to zero-dimensional ideals only, see stdfglm) and variants of the Groebner walk conversion algorithm (which works for arbitrary ideals, See frwalk, grwalk_lib). An implementation of the Hilbert-driven Buchberger algorithm is accessible via the stdhilb command (see also std).

For the ideal below, stdfglm is more than 100 times and stdhilb about 10 times faster than std. The option(pure_gb) avoids the otherwise automatic swich to stdhilb in the std calls.

ring r =32003,(a,b,c,d,e),lp; ideal i=a+b+c+d, ab+bc+cd+ae+de, abc+bcd+abe+ade+cde, abc+abce+abde+acde+bcde, abcde-1; int t=timer; option(prot,pure_gb); ideal j1=stdfglm(i); ==> std in (ZZ/32003),(a,b,c,d,e),(dp(5),C) ==> [1048575:3]1(4)s2(3)s3(2)s4s(3)s5s(4)s(5)s(6)6-ss(7)s(9)s(11)-7-ss(13)s(1\ 5)s(17)--s--8-s(16)s(18)s(20)s(23)s(26)-s(23)-------9--s(16)s10(19)s(22)s\ (25)----s(24)--s11---------s12(17)s(19)s(21)------s(17)s(19)s(21)s13(23)s\ --s-----s(20)----------14-s(12)--------15-s(6)--16-s(5)--17--- ==> (S:21)--------------------- ==> product criterion:109 chain criterion:322 ==> .....+....-...-..-+-....-...-..---...-++---++---....-...-++---.++-----------...------....-...------+--------+---.++------++++-+++----------------+--- ==> vdim= 45 ==> .............................................++--------------------------------------------+--------------------------------------------+--------------------------------------------+-------------------------------------------- timer-t; ==> 0 size(j1); // size (no. of polys) in computed GB ==> 5 t=timer; ideal j2=stdhilb(i); ==> compute hilbert series with std in ring (ZZ/32003),(a,b,c,d,e,@),(dp(6),C\ ) ==> weights used for hilbert series: 1,1,1,1,1,1 ==> [1048575:2]1(4)s2(3)s3(2)s4ss5(3)s(4)s(5)-s6s(6)s(7)s(9)s(11)-7-ss(13)s(1\ 5)s(17)--s--8-s(16)s(18)s(20)s(23)s(26)-s(29)-------9-s(25)s(28)--s(29)--\ -s-------10-s(24)-------s(19)---11-s(17)s(19)s(21)-----s(18)-s(19)s12(21)\ s(23)s(26)-s(27)------s(23)----------13-s(15)-----------14-s(6)--15-s(5)-\ -16--- ==> product criterion:88 chain criterion:650 ==> std with hilb in (ZZ/32003),(a,b,c,d,e,@),(lp(5),dp(1),C) ==> [1048575:2]1(41)s2(40)s3(39)s4s(40)-s5(41)s(44)s(46)s-s--s6s(49)s(51)s(54\ )s(55)s(56)s(58)s(59)--shhhhhhh7(53)s(55)s(57)s(59)s(61)-s(62)s(68)s(70)s\ (71)s(74)--shhhhhhhhhhhhhhhh8(58)s(61)s(65)s(68)s(71)-s(72)s(75)--------s\ hhhhhhhhhhhhhhhhhhh9(51)s(53)s(56)s(58)s(61)s(64)------s(61)s(64)shhhhhhh\ hhhhhhhh10(53)s(55)s(58)s(62)s(64)s(67)s(70)--s(71)------s(68)s(71)s(73)-\ -shhhhhhhhhhhhhhhh11(58)s(60)s(63)s(66)s(69)s(72)s(74)---s-s(76)s(79)----\ s(78)-------shhhhhhhhhhhhhhhhhhhhhhh12(51)s(54)s(57)s(58)s(60)s(63)s(65)s\ (68)s(70)s(73)s(76)s(79)--s(80)----shhhhhhhhhhhhhhhhhhhhhhhhhhhhhh13(48)s\ (51)s(54)s(57)s(59)s(61)s(64)s(67)shhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh\ h14(31)s(33)s(36)s(39)s(42)s(45)shhhhhhhhhhhhhhhhhhhhhhhhh15(23)s(26)s(29\ )s(32)s(35)shhhhhhhhhhhhhhhhhhh16(18)s(21)s(24)s(27)shhhhhhhhhhhhhhh17(15\ )s(18)s(21)s(24)shhhhhhhhhhhh18(15)s(18)s(21)s(24)shhhhhhhhhhhh19(14)s(17\ )s(20)shhhhhhhhhhhh20(11)s(14)s(17)shhhhhhhhh21(11)s(14)s(17)shhhhhhhhh22\ (11)s(14)s(16)shhhhhhhhh23(10)s(13)shhhhhhhhh24(7)s(10)shhhhhh25(7)s(10)s\ hhhhhh26(7)s(10)shhhhhh27(7)s(10)shhhhhh28(7)s(10)shhhhhh29(7)s(10)shhhhh\ h30(7)s(9)shhhhhh31(6)shhhhhh32(3)shhh33shhh34shhh35shhh36shhh37shhh38shh\ h39shhh40shhh41shhh42shhh43shhh44shhh45shhh46shhh47shhh48shhh49shhh50shhh\ 51shhh52shhh53shhh54shhhhhh ==> product criterion:491 chain criterion:11799 ==> hilbert series criterion:416 ==> dehomogenization ==> simplification ==> imap to ring (ZZ/32003),(a,b,c,d,e),(lp(5),C) timer-t; ==> 0 size(j2); // size (no. of polys) in computed GB ==> 5 // usual Groebner basis computation for lex ordering t=timer; ideal j0 =std(i); ==> [1048575:2]1(4)s2(3)s3(2)s4s(3)s5(5)s(4)s6(6)s(7)s(9)s(8)sss7(10)s(11)s(1\ 0)s(11)s(13)s8(12)s(13)s(15)s.s(14).s.9.s(16)s(17)s(19)........10.s(20).s\ (21)ss..11.s(23)s(25).ss(27)...s(28)s(26)...12.s(25)sss(23)sss.......s(22\ )...13.s(23)ssssssss(21)s(22)sssss(21)ss..14.ss(22)s.s.sssss(21)s(22)sss.\ s...15.ssss(21)s(22)ssssssssss(21)s(22)sss16.ssssssss(21)s(22)sssssssssss\ 17ss(21)s(22)ssssssssss(21)sss(22)ss(21)ss18(22)s(21)s(22)s.s............\ ..19.sssss(21)ss(22)ssssssssss(21)s(22)s20.ssssssssss(21)s........21.s(22\ )sssssssssssssss(21)s(22)ssss22ssssssssssss(21)s(22)sssssss23sssssssssss(\ 21)s(22)ssssssss24ssssssssssss(21)s(22)sssssss25ssssssssss(21)s(22)ssssss\ sss26ssssssssss(21)s(20)ssssssss27.sssssssss..........s28.ssssss.........\ ....29.sssssssssssssssssss30sssssssssssssssssss31.sssssssssssssssssss32.s\ sssssssssssssssssss33ssssssssssssssssssss34ssssssssssssssssssss35ssssssss\ ssssssssssss36ssssssssssssssssssss37ssssssssssssssssssss38sssssssssssssss\ sssss39ssssssssssssssssssss40ssssssssssssssssssss41ssss---------------42-\ s(4)--43-s44s45s46s47s48s49s50s51s52s53s54s55s56s ==> product criterion:1395 chain criterion:904 timer-t; ==> 0 option(nopure_gb); t=timer; ideal j0 =std(i); ==> // ** redefining j0 ( ideal j0 =std(i);) ./examples/Groebner_basis_conve\ rsion.sing:19 ==> std in char. 32003, homogenized ------------------ ==> [1048575:2]1(4)s2(3)s3(2)s4ss5(3)s(4)s(5)-s6s(6)s(7)s(9)s(11)-7-ss(13)s(1\ 5)s(17)--s--8-s(16)s(18)s(20)s(23)s(26)-s(29)-------9-s(25)s(28)--s(29)--\ s(30)--------10-s(24)-------s(19)---11-s(17)s(19)s(21)------s(18)s(20)s12\ (22)s(24)s(27)------s(23)-s(24)----------13-s(16)------------14-s(6)--15-\ s(5)--16--- ==> product criterion:88 chain criterion:649 ==> stdhilb in basering, homogenized ------------------ ==> [1048575:2]1(4)s2(3)s3(2)s4s(3)s5(5)s(8)s(10)s-ss6(12)s(15)s(17)s(20)s(21\ )s(22)s(24)s(25)--shhh7(23)s(25)s(27)s(29)s(31)-s(32)s(38)s(40)s(41)s(44)\ --shhhhhhhhhhh8(33)s(36)s(40)s(43)s(46)-s(47)s(50)--------shhhhhhhhhhhhh9\ (32)s(34)s(37)s(39)s(42)s(45)------s(42)s(45)shhhhhhhhhhh10(38)s(40)s(43)\ s(47)s(49)s(52)s(55)--s(56)------s(53)s(56)s(58)--shhhhhhhhhhhhhh11(45)s(\ 47)s(50)s(53)s(56)s(59)s(61)---s-s(63)s(66)----s(65)-------shhhhhhhhhhhhh\ hhhh12(44)s(47)s(50)s(51)s(53)s(56)s(58)s(61)s(63)s(66)s(69)s(72)--s(73)-\ ---shhhhhhhhhhhhhhhhhhhhhhhhhh13(45)s(48)s(51)s(54)s(56)s(58)s(61)s(64)sh\ hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh14(29)s(31)s(34)s(37)s(40)s(43)shhhh\ hhhhhhhhhhhhhhhhhhhh15(22)s(25)s(28)s(31)s(34)shhhhhhhhhhhhhhhhhh16(18)s(\ 21)s(24)s(27)shhhhhhhhhhhhhhh17(15)s(18)s(21)s(24)shhhhhhhhhhhh18(15)s(18\ )s(21)s(24)shhhhhhhhhhhh19(14)s(17)s(20)shhhhhhhhhhhh20(11)s(14)s(17)shhh\ hhhhhh21(11)s(14)s(17)shhhhhhhhh22(11)s(14)s(16)shhhhhhhhh23(10)s(13)shhh\ hhhhhh24(7)s(10)shhhhhh25(7)s(10)shhhhhh26(7)s(10)shhhhhh27(7)s(10)shhhhh\ h28(7)s(10)shhhhhh29(7)s(10)shhhhhh30(7)s(9)shhhhhh31(6)shhhhhh32(3)shhh3\ 3shhh34shhh35shhh36shhh37shhh38shhh39shhh40shhh41shhh42shhh43shhh44shhh45\ shhh46shhh47shhh48shhh49shhh50shhh51shhh52shhh53shhh54shhhhhh ==> product criterion:491 chain criterion:11799 ==> hilbert series criterion:382 ==> de-homogenize, interred ------------------ timer-t; ==> 0 option(noprot);