| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
B.2.5 Module orderings
SINGULAR offers also orderings on the set of "monomials"
![]() in Loc
in Loc ![]() = Loc
= Loc
![]() Loc
Loc ![]() , where
, where
![]() denote the canonical
generators of Loc
denote the canonical
generators of Loc ![]() , the r-fold direct sum of Loc
, the r-fold direct sum of Loc ![]() .
(The function gen(i) yields
.
(The function gen(i) yields ![]() ).
).
We have two possibilities: either to give priority to the component of a
vector in
Loc ![]() or (which is the default in SINGULAR) to give priority
to the coefficients.
The orderings
or (which is the default in SINGULAR) to give priority
to the coefficients.
The orderings (<,c) and (<,C) give priority to the
coefficients; whereas
(c,<) and (C,<) give priority to the components.
Let < be any of the monomial orderings of
Loc ![]() as above.
as above.
- (<,C):
-
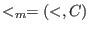 denotes the module ordering (giving priority to the coefficients):
denotes the module ordering (giving priority to the coefficients):
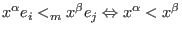 or (
or (
 and
and 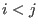 ).
).Example:
ring r = 0, (x,y,z), ds; // the same as ring r = 0, (x,y,z), (ds, C); [x+y2,z3+xy]; ==> x*gen(1)+xy*gen(2)+y2*gen(1)+z3*gen(2) [x,x,x]; ==> x*gen(3)+x*gen(2)+x*gen(1)
- (C,<):
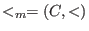 denotes the module ordering (giving priority to the component):
denotes the module ordering (giving priority to the component):
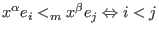 or (
or (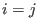 and
and
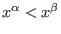 ).
).Example:
ring r = 0, (x,y,z), (C,lp); [x+y2,z3+xy]; ==> xy*gen(2)+z3*gen(2)+x*gen(1)+y2*gen(1) [x,x,x]; ==> x*gen(3)+x*gen(2)+x*gen(1)
- (<,c):
-
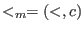 denotes the module ordering (giving priority to the coefficients):
denotes the module ordering (giving priority to the coefficients):
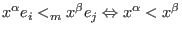 or (
or (
 and
and 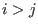 ).
).Example:
ring r = 0, (x,y,z), (lp,c); [x+y2,z3+xy]; ==> xy*gen(2)+x*gen(1)+y2*gen(1)+z3*gen(2) [x,x,x]; ==> x*gen(1)+x*gen(2)+x*gen(3)
- (c,<):
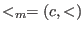 denotes the module ordering (giving priority to the component):
denotes the module ordering (giving priority to the component):
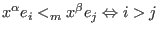 or (
or (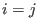 and
and
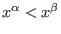 ).
).Example:
ring r = 0, (x,y,z), (c,lp); [x+y2,z3+xy]; ==> [x+y2,xy+z3] [x,x,x]; ==> [x,x,x]
The output of a vector ![]() in
in ![]() with components
with components
![]() has the format
has the format
![]() (up to permutation) unless the ordering starts with
(up to permutation) unless the ordering starts with c.
In this case a vector is written as
![]() .In all cases SINGULAR can read input in both formats.
.In all cases SINGULAR can read input in both formats.