
| Classify |
| Coding |
| Deformations |
| Equidim Part |
| Existence |
| Finite Groups |
| Flatness |
| Genus |
| Hilbert Series |
| Membership |
| Monodromy |
| Normalization |
| Primdec |
| Puiseux |
| Plane Curves |
| Solving |
| Space Curves |
| Spectrum |
Let M be a graded module over K[x1,...,xn] with respect to weights w1,...,wn .
The Hilbert function HM is defined (on Z) by HM(k) := dimKMk .
The Hilbert-Poincaré series of M is the power series
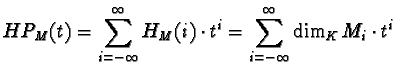

where Q(t) and P(t) are polynomials with coefficients in Z.
- Q(t) is called the first Hilbert series,
- P(t) is called the second Hilbert series.
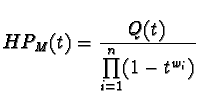
where Q(t) is a polynomial in Z[t], the first (weighted) Hilbert series of M .