| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
2.3.2 Rings and standard bases
In order to compute with objects such as ideals, matrices, modules, and polynomial vectors, a ring has to be defined first.
ring r = 0,(x,y,z),dp; |
The definition of a ring consists of three parts: the first part
determines the ground field, the second part determines the names of the
ring variables, and the third part determines the monomial ordering to
be used. Thus, the above example declares a polynomial ring called r
with a ground field of characteristic
![]() (i.e., the rational
numbers) and ring variables called
(i.e., the rational
numbers) and ring variables called x, y, and z. The
dp at the end determines that the degree reverse lexicographical
ordering will be used.
Other ring declarations:
ring r1=32003,(x,y,z),dp;- characteristic 32003, variables
x,y, andzand orderingdp. ring r2=32003,(a,b,c,d),lp;- characteristic 32003, variable names
a,b,c,dand lexicographical ordering. ring r3=7,(x(1..10)),ds;- characteristic 7, variable names
x(1),...,x(10), negative degree reverse lexicographical ordering (ds). ring r4=(0,a),(mu,nu),lp;- transcendental extension of
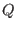 by
by
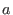 , variable names
, variable names
muandnu, lexicographical ordering. ring r5=real,(a,b),lp;- floating point numbers (single machine precision),
variable names
aandb. ring r6=(real,50),(a,b),lp;- floating point numbers with precision extended to 50 digits,
variable names
aandb. ring r7=(complex,50,i),(a,b),lp;- complex floating point numbers with precision extended to 50 digits
and imaginary unit
i, variable namesaandb. ring r8=integer,(a,b),lp;- the ring of integers (see Coefficient rings),
variable names
aandb. ring r9=(integer, 60),(a,b),lp;- the ring of integers modulo 60 (see Coefficient rings),
variable names
aandb. ring r10=(integer, 2, 10),(a,b),lp;- the ring of integers modulo 2^10 (see Coefficient rings),
variable names
aandb.
Typing the name of a ring prints its definition. The example below
shows that the default ring in SINGULAR is
![]() with
degree reverse lexicographical ordering:
with
degree reverse lexicographical ordering:
ring r11; r11; ==> // coefficients: ZZ/32003 considered as a field ==> // number of vars : 3 ==> // block 1 : ordering dp ==> // : names x y z ==> // block 2 : ordering C |
Defining a ring makes this ring the current active basering, so each ring definition above switches to a new basering. The concept of rings in SINGULAR is discussed in detail in Rings and orderings.
The basering is now r11. Since we want to calculate in the ring
r, which we defined first, we need to switch back to it. This can
be done using the function setring:
setring r; |
Once a ring is active, we can define polynomials. A monomial, say
![]() may be entered in two ways: either using the power operator
may be entered in two ways: either using the power operator ^,
writing x^3, or in short-hand notation without operator, writing
x3. Note that the short-hand notation is forbidden if a name
of the ring variable(s) consists of more than one character(see Miscellaneous oddities for details).
Note, that SINGULAR always expands brackets and automatically
sorts the terms with respect to the monomial ordering of the basering.
poly f = x3+y3+(x-y)*x2y2+z2; f; ==> x3y2-x2y3+x3+y3+z2 |
The command size retrieves in general the number of entries in
an object. In particular, for polynomials, size returns the
number of monomials.
size(f); ==> 5 |
A natural question is to ask if a point, e.g., (x,y,z)=(1,2,0), lies
on the variety defined by the polynomials f and g. For
this we define an ideal generated by both polynomials, substitute the
coordinates of the point for the ring variables, and check if the result
is zero:
poly g = f^2 *(2x-y); ideal I = f,g; ideal J = subst(I,var(1),1); J = subst(J,var(2),2); J = subst(J,var(3),0); J; ==> J[1]=5 ==> J[2]=0 |
Since the result is not zero, the point (1,2,0) does
not lie on the variety V(f,g).
Another question is to decide whether some function vanishes on a
variety, or in algebraic terms, if a polynomial is contained in a given
ideal. For this we calculate a standard basis using the command
groebner and afterwards reduce the polynomial with respect to
this standard basis.
ideal sI = groebner(f); reduce(g,sI); ==> 0 |
As the result is 0 the polynomial g belongs to the
ideal defined by f.
The function groebner, like many other functions in
SINGULAR, prints a protocol during calculations, if desired. The
command option(prot); enables protocolling whereas
option(noprot); turns it off.
option, explains the meaning
of the different symbols printed during calculations.
The command kbase calculates a basis of the polynomial ring
modulo an ideal, if the quotient ring is finite dimensional.
As an example we calculate the Milnor number of a
hypersurface singularity in the global and local case. This is the
vector space dimension of the polynomial ring modulo the Jacobian ideal
in the global case resp. of the power series ring modulo the Jacobian
ideal in the local case. See Critical points, for a detailed
explanation.
The Jacobian ideal is obtained with the command jacob.
ideal J = jacob(f); ==> // ** redefining J ** J; ==> J[1]=3x2y2-2xy3+3x2 ==> J[2]=2x3y-3x2y2+3y2 ==> J[3]=2z |
SINGULAR prints the line // ** redefining J
**. This indicates that we had previously defined a variable with name
J of type ideal (see above).
To obtain a representing set of the quotient vector space we first
calculate a standard basis, and then apply the function kbase to
this standard basis.
J = groebner(J); ideal K = kbase(J); K; ==> K[1]=y4 ==> K[2]=xy3 ==> K[3]=y3 ==> K[4]=xy2 ==> K[5]=y2 ==> K[6]=x2y ==> K[7]=xy ==> K[8]=y ==> K[9]=x3 ==> K[10]=x2 ==> K[11]=x ==> K[12]=1 |
Then
size(K); ==> 12 |
gives the desired vector space dimension
![]() .As in SINGULAR the functions may take the input directly from
earlier calculations, the whole sequence of commands may be written
in one single statement.
.As in SINGULAR the functions may take the input directly from
earlier calculations, the whole sequence of commands may be written
in one single statement.
size(kbase(groebner(jacob(f)))); ==> 12 |
When we are not interested in a basis of the quotient vector space, but
only in the resulting dimension we may even use the command vdim
and write:
vdim(groebner(jacob(f))); ==> 12 |