| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
A.2.2 Groebner basis conversion
The performance of Buchberger's algorithm is sensitive to the chosen monomial order. A Groebner basis computation with respect to a less favorable order such as the lexicographic ordering may easily run out of time or memory even in cases where a Groebner basis computation with respect to a more efficient order such as the degree reverse lexicographic ordering is very well feasible. Groebner basis conversion algorithms and the Hilbert-driven Buchberger algorithm are based on this observation:
-
Groebner basis conversion: Given an ideal
![$I\subset K[x_1,\dots,x_n]$](sing_438.png) and a
slow monomial order, compute a Groebner basis with respect to an
appropriately chosen fast order. Then convert the result to a Groebner
basis with respect to the given slow order.
and a
slow monomial order, compute a Groebner basis with respect to an
appropriately chosen fast order. Then convert the result to a Groebner
basis with respect to the given slow order.
-
Hilbert-driven Buchberger algorithm: Homogenize the given
generators for
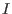 with respect to a new variable, say,
with respect to a new variable, say,
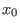 .
Extend the given slow ordering on
.
Extend the given slow ordering on
![$K[x_1,\dots,x_n]$](sing_440.png) to a global
product ordering on
to a global
product ordering on
![$K[x_0,\dots,x_n]$](sing_441.png) .
Compute a Groebner basis for the ideal generated by the homogenized
polynomials with respect to a fast ordering. Read the Hilbert function, and
use this information when computing a Groebner basis with
respect to the extended (slow) ordering. Finally,
dehomogenize the elements of the resulting Groebner basis.
.
Compute a Groebner basis for the ideal generated by the homogenized
polynomials with respect to a fast ordering. Read the Hilbert function, and
use this information when computing a Groebner basis with
respect to the extended (slow) ordering. Finally,
dehomogenize the elements of the resulting Groebner basis.
SINGULAR provides implementations for the FGLM conversion algorithm
(which applies to zero-dimensional ideals only, see stdfglm) and
variants of the Groebner walk conversion algorithm (which works for
arbitrary ideals, See frwalk, grwalk_lib).
An implementation of the Hilbert-driven Buchberger
algorithm is accessible via the stdhilb command (see also std).
For the ideal below, stdfglm is more than 100 times
and stdhilb about 10 times faster than std.
ring r =32003,(a,b,c,d,e),lp;
ideal i=a+b+c+d, ab+bc+cd+ae+de, abc+bcd+abe+ade+cde,
abc+abce+abde+acde+bcde, abcde-1;
int t=timer;
option(prot);
ideal j1=stdfglm(i);
==> std in (ZZ/32003),(a,b,c,d,e),(dp(5),C)
==> [1048575:3]1(4)s2(3)s3(2)s4s(3)s5s(4)s(5)s(6)6-ss(7)s(9)s(11)-7-ss(13)s(1\
5)s(17)--s--8-s(16)s(18)s(20)s(23)s(26)-s(23)-------9--s(16)s10(19)s(22)s\
(25)----s(24)--s11---------s12(17)s(19)s(21)------s(17)s(19)s(21)s13(23)s\
--s-----s(20)----------14-s(12)--------15-s(6)--16-s(5)--17---
==> (S:21)---------------------
==> product criterion:109 chain criterion:322
==> .....+....-...-..-+-....-...-..---...-++---++---....-...-++---.++-----------...------....-...------+--------+---.++------++++-+++----------------+---
==> vdim= 45
==> .............................................++--------------------------------------------+--------------------------------------------+--------------------------------------------+--------------------------------------------
timer-t;
==> 0
size(j1); // size (no. of polys) in computed GB
==> 5
t=timer;
ideal j2=stdhilb(i);
==> compute hilbert series with std in ring (ZZ/32003),(a,b,c,d,e,@),(dp(6),C\
)
==> weights used for hilbert series: 1,1,1,1,1,1
==> [1048575:2]1(4)s2(3)s3(2)s4ss5(3)s(4)s(5)-s6s(6)s(7)s(9)s(11)-7-ss(13)s(1\
5)s(17)--s--8-s(16)s(18)s(20)s(23)s(26)-s(29)-------9-s(25)s(28)--s(29)--\
-s-------10-s(24)-------s(19)---11-s(17)s(19)s(21)-----s(18)-s(19)s12(21)\
s(23)s(26)-s(27)------s(23)----------13-s(15)-----------14-s(6)--15-s(5)-\
-16---
==> product criterion:88 chain criterion:650
==> std with hilb in (ZZ/32003),(a,b,c,d,e,@),(lp(5),dp(1),C)
==> [1048575:2]1(41)s2(40)s3(39)s4s(40)-s5(41)s(44)s(46)s-s-sh6s(49)s(51)s(54\
)s(55)s(56)s(58)s(59)--shhhhhhh7(53)s(55)s(57)s(59)s(61)-s(62)s(68)s(70)s\
(71)s(74)--shhhhhhhhhhhhhhhh8(58)s(61)s(65)s(68)s(71)-s(72)s(75)--------s\
hhhhhhhhhhhhhhhhhhh9(51)s(53)s(56)s(58)s(61)s(64)------s(61)s(64)shhhhhhh\
hhhhhhhh10(53)s(55)s(58)s(62)s(64)s(67)s(70)--s(71)------s(68)s(71)s(73)-\
-shhhhhhhhhhhhhhhh11(58)s(60)s(63)s(66)s(69)s(72)s(74)---s-s(76)s(79)----\
s(78)-------shhhhhhhhhhhhhhhhhhhhhhh12(51)s(54)s(57)s(58)s(60)s(63)s(65)s\
(68)s(70)s(73)s(76)s(79)--s(80)----shhhhhhhhhhhhhhhhhhhhhhhhhhhhhh13(48)s\
(51)s(54)s(57)s(59)s(61)s(64)s(67)shhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh\
h14(31)s(33)s(36)s(39)s(42)s(45)shhhhhhhhhhhhhhhhhhhhhhhhh15(23)s(26)s(29\
)s(32)s(35)shhhhhhhhhhhhhhhhhhh16(18)s(21)s(24)s(27)shhhhhhhhhhhhhhh17(15\
)s(18)s(21)s(24)shhhhhhhhhhhh18(15)s(18)s(21)s(24)shhhhhhhhhhhh19(14)s(17\
)s(20)shhhhhhhhhhhh20(11)s(14)s(17)shhhhhhhhh21(11)s(14)s(17)shhhhhhhhh22\
(11)s(14)s(16)shhhhhhhhh23(10)s(13)shhhhhhhhh24(7)s(10)shhhhhh25(7)s(10)s\
hhhhhh26(7)s(10)shhhhhh27(7)s(10)shhhhhh28(7)s(10)shhhhhh29(7)s(10)shhhhh\
h30(7)s(9)shhhhhh31(6)shhhhhh32(3)shhh33shhh34shhh35shhh36shhh37shhh38shh\
h39shhh40shhh41shhh42shhh43shhh44shhh45shhh46shhh47shhh48shhh49shhh50shhh\
51shhh52shhh53shhh54shhhhhh
==> product criterion:491 chain criterion:11799
==> hilbert series criterion:417
==> dehomogenization
==> simplification
==> imap to ring (ZZ/32003),(a,b,c,d,e),(lp(5),C)
timer-t;
==> 0
size(j2); // size (no. of polys) in computed GB
==> 5
// usual Groebner basis computation for lex ordering
t=timer;
ideal j0 =std(i);
==> [1048575:2]1(4)s2(3)s3(2)s4s(3)s5(5)s(4)s6(6)s(7)s(9)s(8)sss7(10)s(11)s(1\
0)s(11)s(13)s8(12)s(13)s(15)s.s(14).s.9.s(16)s(17)s(19)........10.s(20).s\
(21)ss..11.s(23)s(25).ss(27)...s(28)s(26)...12.s(25)sss(23)sss.......s(22\
)...13.s(23)ssssssss(21)s(22)sssss(21)ss..14.ss(22)s.s.sssss(21)s(22)sss.\
s...15.ssss(21)s(22)ssssssssss(21)s(22)sss16.ssssssss(21)s(22)sssssssssss\
17ss(21)s(22)ssssssssss(21)sss(22)ss(21)ss18(22)s(21)s(22)s.s............\
..19.sssss(21)ss(22)ssssssssss(21)s(22)s20.ssssssssss(21)s........21.s(22\
)sssssssssssssss(21)s(22)ssss22ssssssssssss(21)s(22)sssssss23sssssssssss(\
21)s(22)ssssssss24ssssssssssss(21)s(22)sssssss25ssssssssss(21)s(22)ssssss\
sss26ssssssssss(21)s(20)ssssssss27.sssssssss..........s28.ssssss.........\
....29.sssssssssssssssssss30sssssssssssssssssss31.sssssssssssssssssss32.s\
sssssssssssssssssss33ssssssssssssssssssss34ssssssssssssssssssss35ssssssss\
ssssssssssss36ssssssssssssssssssss37ssssssssssssssssssss38sssssssssssssss\
sssss39ssssssssssssssssssss40ssssssssssssssssssss41ssss---------------42-\
s(4)--43-s44s45s46s47s48s49s50s51s52s53s54s55s56s
==> product criterion:1395 chain criterion:904
option(noprot);
timer-t;
==> 0
|