|
|
7.4.1 G-algebras
Definition (PBW basis)
Let 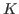 be a field, and let a be a field, and let a 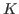 -algebra -algebra 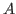 be generated by
variables be generated by
variables
 subject to some relations.
We call subject to some relations.
We call 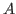 an algebra with PBW basis (Poincaré-Birkhoff-Witt basis), if a an algebra with PBW basis (Poincaré-Birkhoff-Witt basis), if a 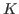 -basis of -basis of
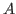 is Mon is Mon
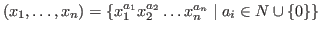 ,
where a power-product ,
where a power-product
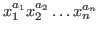 (in this particular order) is called
a monomial. For example, (in this particular order) is called
a monomial. For example, 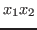 is a monomial, while is a monomial, while 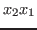 is, in general, not
a monomial. is, in general, not
a monomial.
Definition (G-algebra)
Let 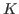 be a field, and let a be a field, and let a 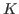 -algebra -algebra 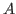 be given in terms of generators subject to the following relations: be given in terms of generators subject to the following relations:
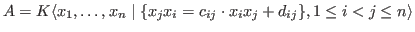 ,
where ,
where
![$c_{ij} \in K^{*}, d_{ij} \in K[x_1, \ldots, x_n]$](sing_222.png) . .
 is called a is called a  -algebra, if the following conditions hold: -algebra, if the following conditions hold:
-
there is a monomial well-ordering
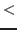 on on
![$K[x_1,x_2,\ldots,x_n]$](sing_224.png) such that such that
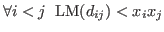 , ,
- non-degeneracy conditions:
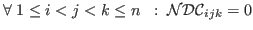 , where , where
Note: Note that non-degeneracy conditions simply ensure associativity of multiplication.
Theorem (properties of G-algebras)
Let 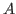 be a be a 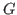 -algebra. Then -algebra. Then
-
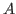 has a PBW (Poincaré-Birkhoff-Witt) basis, has a PBW (Poincaré-Birkhoff-Witt) basis,
-
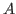 is left and right noetherian,
is left and right noetherian,
-
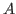 is an integral domain. is an integral domain.
Setting up a G-algebra
In order to set up a 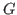 -algebra one has to do the following steps: -algebra one has to do the following steps:
At present, PLURAL does not check automatically whether the non-degeneracy conditions
hold but it provides a procedure ndcond from the library nctools_lib to check this.
|
 Online Manual
Online Manual