C.6.2.4 The algorithm of Di Biase and Urbanke
Like the algorithm of Hosten and Sturmfels, the algorithm of Di Biase
and Urbanke (see [DBUr95]) performs up
to 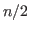 Groebner basis
computations. It needs no auxiliary variables, but a supplementary
precondition; namely, the existence of a vector without zero components
in the kernel of Groebner basis
computations. It needs no auxiliary variables, but a supplementary
precondition; namely, the existence of a vector without zero components
in the kernel of 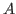 . .
The main idea comes from the following observation:
Let 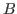 be an integer matrix, be an integer matrix,
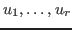 a lattice basis of the
integer kernel of a lattice basis of the
integer kernel of 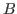 . Assume that all components of . Assume that all components of 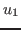 are
positive. Then are
positive. Then
i.e., the ideal on the right is already saturated w.r.t. all variables.
The algorithm starts by finding a lattice basis
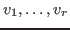 of the
kernel of of the
kernel of 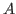 such that such that 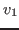 has no zero component. Let has no zero component. Let
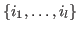 be the set of indices be the set of indices 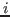 with with
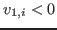 . Multiplying the components . Multiplying the components
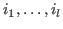 of of
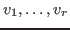 and the columns and the columns
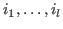 of of  by by 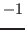 yields
a matrix yields
a matrix 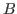 and a lattice basis and a lattice basis
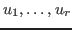 of the kernel of of the kernel of 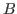 that fulfill the assumption of the observation above. It is then possible
to compute a generating set of
that fulfill the assumption of the observation above. It is then possible
to compute a generating set of 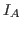 by applying the following
``variable flip'' successively to by applying the following
``variable flip'' successively to
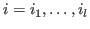 : :
Let 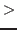 be an elimination ordering for be an elimination ordering for 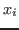 . Let . Let 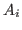 be the matrix
obtained by multiplying the be the matrix
obtained by multiplying the 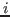 -th column of -th column of 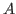 by by 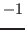 . Let . Let
be a Groebner basis of 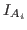 w.r.t. w.r.t. 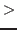 (where (where 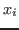 is neither
involved in is neither
involved in 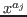 nor in nor in 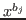 ). Then ). Then
is a generating set for 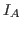 . .
|
 Online Manual
Online Manual