This library implements functional uni-multivariate decomposition
of multivariate polynomials.
A (multivariate) polynomial f is a composite if it can be written as
 where g is univariate and h is multivariate,
where
where g is univariate and h is multivariate,
where
 .
.
Uniqueness for monic polynomials is up to linear coordinate change
 .
.
If f is a composite, then decompose(f); returns an ideal (g,h);
such that
 is maximal, (
is maximal, (
 ).
The polynomial h is, by the maximality of
).
The polynomial h is, by the maximality of
 , not a composite.
, not a composite.
The polynomial g is univariate in the (first) variable vvar of f,
such that deg_vvar(f) is maximal.
decompose(f,1); computes a full decomposition, i.e. if f is a
composite, then an ideal
 is returned, where
is returned, where
 are univariate and each entry is primitive such that
are univariate and each entry is primitive such that
 .
.
If f is not a composite, for instance if
 is prime,
then
is prime,
then decompose(f); returns f.
The command decompose is the inverse: compose(decompose(f,1))==f.
Recall, that Chebyshev polynomials of the first kind commute by composition.
The decomposition algorithms work in the tame case, that is if
char(basering)=0 or p:=char(basering) > 0 but deg(g) is not divisible by
p.
Additionally, it works for monic polynomials over
 and in some
cases for monic polyomials over coefficient rings.
and in some
cases for monic polyomials over coefficient rings.
See
is_composite for examples. (It also works over the reals but
there it seems not be numerical stable.)
More information on the univariate resp. multivariate case.
Univariate decomposition is created, with the additional assumption
 .
.
A multivariate polynomial f is a composite, if f can be written as
 , where
, where
 is a univariate polynomial and
is a univariate polynomial and
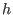
is multivariate. Note, that unlike in the univariate case, the polynomial
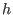 may be of degree
may be of degree
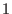 .
.
E.g.
 is the composite of
is the composite of
 and
and
 .
.
If nvars(basering)>1, then, by default, a single-variable
multivariate polynomial is not considered to be the same as in the
one-variable polynomial ring; it will always be decomposed. That is:
> ring r1=0,x,dp;
> decompose(x3+2x+1);
x3+2x+1
but:
> ring r2=0,(x,y),dp;
> decompose(x3+2x+1);
_[1]=x3+2x+1
_[2]=x
In particular:
is_composite(x3+2x+1)==1; in ring r1 but
is_composite(x3+2x+1)==0; in ring r2.
This is justified by interpreting the polynomial decomposition as an
affine Stein factorization of the mapping
 .
.
The behaviour can changed by the some global variables.
int DECMETH; choose von zur Gathen's or Kozen-Landau's method.
int MINS; compute f = g o h, such that h(0) = 0.
int IMPROVE; simplify the coefficients of g and h if f is
not monic.
int DEGONE; single-variable multivariate are
considered uni-variate.
See decompopts; for more information.
Additional information is displayed if printlevel > 0.
D. Kozen, S. Landau: Polynomial Decomposition Algorithms,
J. Symb. Comp. (1989), 7, 445-456.
J. von zu Gathen: Functional Decomposition of Polynomials: the Tame Case,
J. Symb. Comp. (1990), 9, 281-299.
J. von zur Gathen, J. Gerhard: Modern computer algebra,
Cambridge University Press, Cambridge, 2003.