|
|
D.4.26.9 intersectionValRings
Procedure from library normaliz.lib (see normaliz_lib).
- Usage:
- intersectionValRings(intmat V, intvec grading);
- Return:
- The function returns a monomial ideal, to be considered as the list
of monomials generating
 as an algebra over the coefficient
field. as an algebra over the coefficient
field.
- Background:
- A discrete monomial valuation
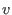 on on
![$R = K[X_1 ,\ldots,X_n]$](sing_1027.png) is determined by
the values is determined by
the values  of the indeterminates. This function computes the
subalgebra of the indeterminates. This function computes the
subalgebra
 for several
such valuations for several
such valuations  , ,  . It needs the matrix . It needs the matrix
 as
its input. as
its input.
The function returns the ideal given by the input matrix V if one of
the options supp, triang, volume, or
hseries has been activated.
However, in this case some numerical invariants are computed, and
some other data may be contained in files that you can read into
Singular (see showNuminvs, exportNuminvs).
Example:
| | LIB "normaliz.lib";
ring R=0,(x,y,z,w),dp;
intmat V0[2][4]=0,1,2,3, -1,1,2,1;
intersectionValRings(V0);
==> _[1]=w
==> _[2]=z
==> _[3]=y
==> _[4]=xw
==> _[5]=xz
==> _[6]=xy
==> _[7]=x2z
|
See also:
diagInvariants;
finiteDiagInvariants;
intersectionValRingIdeals;
torusInvariants.
|