|
|
7.1 PLURAL

A Subsystem for Non-commutative Polynomial G-Algebras
- What is and what does PLURAL?
PLURAL is a kernel extension of SINGULAR,
providing many algorithms for computations within non-commutative
 and and
 algebras
(see Mathematical background (plural) for detailed information on algebras and algorithms). algebras
(see Mathematical background (plural) for detailed information on algebras and algorithms).
It uses the same data structures as SINGULAR, sometimes interpreting them
in a different way and/or modifying them for its own purposes.
In spite of such a difference, one can always transfer
objects between commutative rings of SINGULAR and non-commutative rings of PLURAL.
With PLURAL, one can set up a non-commutative
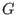 -algebra, say -algebra, say
 , with
a Poincaré-Birkhoff-Witt (PBW) basis, (see G-algebras for step-by-step building instructions
and also PLURAL libraries for procedures for setting many important algebras easily).
Afterwards, one can proceed to the factor-algebra of , with
a Poincaré-Birkhoff-Witt (PBW) basis, (see G-algebras for step-by-step building instructions
and also PLURAL libraries for procedures for setting many important algebras easily).
Afterwards, one can proceed to the factor-algebra of
 modulo a two-sided ideal (see twostd (plural)), thus
obtaining a modulo a two-sided ideal (see twostd (plural)), thus
obtaining a
 -algebra (see qring (plural) type). -algebra (see qring (plural) type).
Functionalities of PLURAL (enlisted in Functions (plural)) are accessible as soon
as the basering becomes non-commutative (see nc_algebra and the library ncalg_lib
with many readily predefined algebras).
One can perform various computations with polynomials and ideals in
 and with
vectors and submodules of a free module and with
vectors and submodules of a free module
 . .
- What PLURAL does not:
-
- PLURAL conventions
- *-multiplication (plural)
in the non-commutative case, the correct multiplication of y by
x must be written as y*x.
Both expressions yx and xy are equal, since they are
interpreted as commutative expressions. See example in poly expressions (plural).
Note, that PLURAL output consists only of standard monomials, even when the signs * are omitted.
ideal (plural)
Unless stated otherwise, an expression of type ideal as understood by PLURAL
as a list of generators of a left ideal. For more information see ideal (plural).
For a two-sided ideal T, use the command twostd (plural) for computing
the two-sided Groebner basis of T.
For a right ideal I, use rightstd (letterplace) from nctools_lib for computing the right
Groebner basis of I.
module (plural)
- Unless stated otherwise, a
module as understood by PLURAL
is either a finitely generated left submodule of a free module (of finite rank)
or a factor module of a free module (of finite rank) by its left submodule (see module (plural) for details). The concrete interpretation left to a function.
qring (plural)
- It is only possible to build factor-algebras modulo two-sided ideals (see qring (plural)), which have
to be given via their two-sided Groebner basis (see twostd (plural)).
|

