|
|
7.9.2 Monomial orderings on free algebras
We provide many types of orderings for non-commutative Groebner bases up to a degree (length) bound.
In general it is not clear, whether a given generating set has a finite Groebner
bases with respect to some ordering.
Let
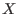 = { = {
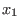 ,..., ,...,
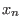 } be a set of symbols. A total ordering < on the free monoid } be a set of symbols. A total ordering < on the free monoid
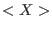 with with
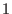 as the neutral element is called a monomial ordering if as the neutral element is called a monomial ordering if
- it is a well-ordering, i.e., every non empty subset has a least element with respect to <, and
- it is compatible with multiplication, that is
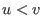 implies implies
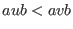 for all for all
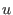 , ,
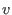 , ,
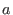 and and
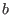 in in
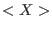 . .
Note that the latter implies
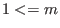 for all for all
 in in
 . .
The left lexicographical ordering on
 with with
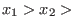 ... ...
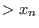 is defined as follows:
For arbitrary is defined as follows:
For arbitrary
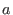 , ,
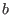 in in
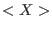 we say that we say that
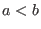 , if , if
Note: left lex is not a monomial ordering, though it is a natural choice to break ties
after, say, comparing elements by the total degree.
In a similar manner one can define the right lexicographical ordering.
On the monoid
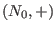 define the weight homomorphism define the weight homomorphism
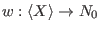 , uniquely determined by , uniquely determined by
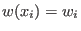 in in
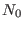 for for
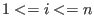 . .
As a special case, define the length
len:
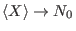 by by
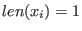 for for
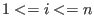 . .
For any ordering << on
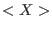 and any weight and any weight
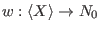 define an ordering define an ordering
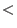 , called the , called the
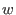 -weight extension of -weight extension of
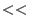 as follows:
For arbitrary as follows:
For arbitrary
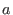 , ,
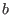 in in
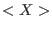 we say that we say that
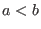 if if
An ordering < on
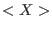 eliminates a certain subset eliminates a certain subset
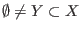 if for all if for all
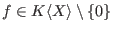 one has one has
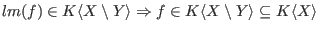 . .
In a ring declaration, LETTERPLACE supports the following monomial orderings.
We illustrate each of the available choices by an example on the free monoid
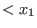 , ,
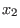 , ,
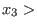 ,
where we order the monomials ,
where we order the monomials
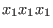 , ,
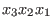 , ,
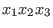 , ,
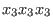 , ,
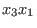 , ,
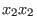 , ,
 , ,
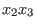 , ,
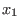 , ,
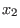 and and
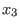 correspondingly. correspondingly.
- `
dp'
- The degree right lexicographical ordering is the length-weight extension of the right lexicographical ordering.
With respect to the ordering `dp', the test monomials are ordered as follows:
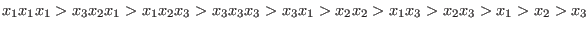
- `
Dp'
- The degree left lexicographical ordering is the length-weight extension of the left lexicographical ordering.
With respect to the ordering `Dp', the test monomials are ordered as follows:
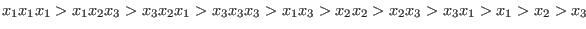
- `
Wp(w) for intvec w'
- The weighted degree left lexicographical ordering is the
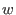 -weight extension of the left lexicographical ordering with weight -weight extension of the left lexicographical ordering with weight
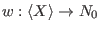 uniquely determined by strict positive uniquely determined by strict positive
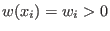 . .
With respect to the ordering `Wp(1, 2, 1)', the test monomials are ordered as follows:
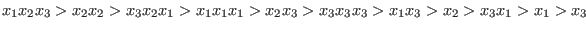
- `
lp'
- Let
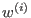 be weights uniquely determined by be weights uniquely determined by
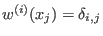 for for
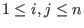 where where 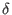 denotes the Kronecker delta. Let denotes the Kronecker delta. Let 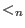 be the be the 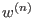 -weight extension of the left lexicographical ordering on -weight extension of the left lexicographical ordering on
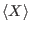 and inductively and inductively 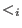 be the be the 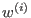 -weight extension of -weight extension of 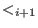 for all for all 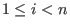 .
The monomial ordering lp corresponds to .
The monomial ordering lp corresponds to 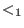 and eliminates and eliminates 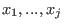 for all for all 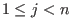 .
We refer to it as to left elimination ordering. .
We refer to it as to left elimination ordering.
The monomial ordering `lp' corresponds to
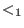 and eliminates { and eliminates {
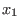 ,..., ,...,
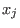 } for all } for all
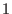 <= <=
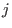 < <
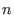 .
We refer to it as to left elimination ordering. .
We refer to it as to left elimination ordering.
With respect to the ordering `lp', the test monomials are ordered as follows:
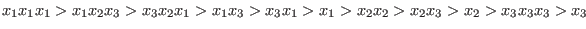
- `
rp'
- Let
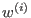 be weights uniquely determined by be weights uniquely determined by
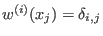 for for
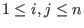 where where 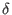 denotes the Kronecker delta. Let denotes the Kronecker delta. Let 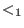 be the be the 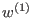 -weight extension of the left lexicographical ordering on -weight extension of the left lexicographical ordering on
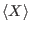 and inductively and inductively 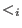 be the be the 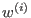 -weight extension of -weight extension of 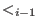 for all for all 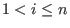 .
The monomial ordering rp corresponds to .
The monomial ordering rp corresponds to 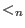 and eliminates and eliminates
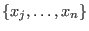 for all for all 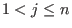 .
We refer to it as to right elimination ordering. .
We refer to it as to right elimination ordering.
The monomial ordering `rp' corresponds to
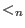 and eliminates { and eliminates {
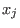 ,..., ,...,
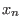 } for all } for all
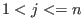 . We refer to it as to right elimination ordering. . We refer to it as to right elimination ordering.
With respect to the ordering `rp', the test monomials are ordered as follows:
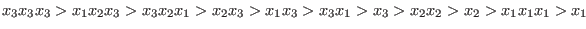
- `
(a(v), ordering) for intvec v'
- For weight
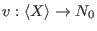 determined by determined by
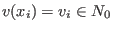 with with 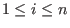 and monomial ordering and monomial ordering 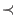 on on
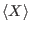 , the , the 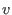 -weight extension of -weight extension of 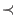 corresponds to (a(v), o). As a choice for corresponds to (a(v), o). As a choice for 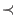 there are currently two options implemented, which are dp and Dp. Notice that this ordering eliminates there are currently two options implemented, which are dp and Dp. Notice that this ordering eliminates
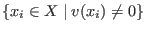 . .
With respect to the ordering `( a(1, 0, 0), Dp)', the test monomials are ordered as follows:
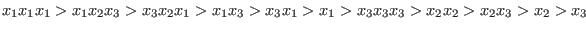
With ordering `( a(1, 1, 0), Dp)' one obtains:
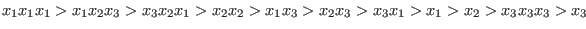
The examples are generated by the following code but with customized orderings denoted above.
| | LIB "freegb.lib";
ring r = 0, (x1,x2,x3),Dp; // variate ordering here
ring R = freeAlgebra(r, 4);
poly wr = x1*x1*x1+x3*x3*x3+x1*x2*x3+x3*x2*x1+x2*x2+x2*x3+x1*x3+x3*x1+x1+x2+x3;
wr; // polynomial will be automatically ordered according to the ordering on R
==> x1*x1*x1+x1*x2*x3+x3*x2*x1+x3*x3*x3+x1*x3+x2*x2+x2*x3+x3*x1+x1+x2+x3
|
|