|
|
A.4.4 T1 and T2
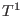 , resp. , resp.
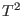 , of an ideal , of an ideal
 usually denote the modules of
infinitesimal deformations, resp. of obstructions.
In SINGULAR there are procedures usually denote the modules of
infinitesimal deformations, resp. of obstructions.
In SINGULAR there are procedures T_1 and T_2 in
sing.lib such that
T_1(j) and T_2(j) compute a standard basis of
a presentation of these modules.
If
 are finite dimensional K-vector spaces (e.g., for isolated
singularities), a basis can be computed by applying are finite dimensional K-vector spaces (e.g., for isolated
singularities), a basis can be computed by applying
kbase(T_1(j));, resp. kbase(T_2(j));, the dimensions by
applying vdim.
For a complete intersection j the procedure Tjurina also
computes
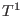 , but faster ( , but faster (
 in this case).
For a non complete intersection, it is faster to use the procedure in this case).
For a non complete intersection, it is faster to use the procedure T_12
instead of T_1 and T_2.
Type help T_1; (or help T_2; or help T_12;) to obtain
more detailed information about these procedures.
We give three examples, the first being a hypersurface, the second a complete
intersection, the third not a complete intersection:
-
load
sing.lib
-
check whether the ideal j is a complete intersection. It is, if
number of variables = dimension + minimal number of generators
-
compute the Tjurina number
-
compute a vector space basis (kbase) of
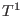
-
compute the Hilbert function of
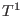
-
create a polynomial encoding the Hilbert series
-
compute the dimension of
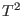
| | LIB "sing.lib";
ring R=32003,(x,y,z),ds;
// ---------------------------------------
// hypersurface case (from series T[p,q,r]):
int p,q,r = 3,3,4;
poly f = x^p+y^q+z^r+xyz;
tjurina(f);
==> 8
// Tjurina number = 8
kbase(Tjurina(f));
==> // Tjurina number = 8
==> _[1]=z3
==> _[2]=z2
==> _[3]=yz
==> _[4]=xz
==> _[5]=z
==> _[6]=y
==> _[7]=x
==> _[8]=1
// ---------------------------------------
// complete intersection case (from series P[k,l]):
int k,l =3,2;
ideal j=xy,x^k+y^l+z2;
dim(std(j)); // Krull dimension
==> 1
size(minbase(j)); // minimal number of generators
==> 2
tjurina(j); // Tjurina number
==> 6
module T=Tjurina(j);
==> // Tjurina number = 6
kbase(T); // a sparse output of the k-basis of T_1
==> _[1]=z*gen(1)
==> _[2]=gen(1)
==> _[3]=y*gen(2)
==> _[4]=x2*gen(2)
==> _[5]=x*gen(2)
==> _[6]=gen(2)
print(kbase(T)); // columns of matrix are a k-basis of T_1
==> z,1,0,0, 0,0,
==> 0,0,y,x2,x,1
// ---------------------------------------
// general case (cone over rational normal curve of degree 4):
ring r1=0,(x,y,z,u,v),ds;
matrix m[2][4]=x,y,z,u,y,z,u,v;
ideal i=minor(m,2); // 2x2 minors of matrix m
module M=T_1(i); // a presentation matrix of T_1
==> // dim T_1 = 4
vdim(M); // Tjurina number
==> 4
hilb(M); // display of both Hilbert series
==> // 4 t^0
==> // -20 t^1
==> // 40 t^2
==> // -40 t^3
==> // 20 t^4
==> // -4 t^5
==>
==> // 4 t^0
==> // dimension (local) = 0
==> // multiplicity = 4
intvec v1=hilb(M,1); // first Hilbert series as intvec
intvec v2=hilb(M,2); // second Hilbert series as intvec
v1;
==> 4,-20,40,-40,20,-4,0
v2;
==> 4,0
v1[3]; // 3rd coefficient of the 1st Hilbert series
==> 40
module N=T_2(i);
==> // dim T_2 = 3
|
| | // In some cases it might be useful to have a polynomial in some ring
// encoding the Hilbert series. This polynomial can then be
// differentiated, evaluated etc. It can be done as follows:
ring H = 0,t,ls;
poly h1;
int ii;
for (ii=1; ii<=size(v1); ii=ii+1)
{
h1=h1+v1[ii]*t^(ii-1);
}
h1; // 1st Hilbert series
==> 4-20t+40t2-40t3+20t4-4t5
diff(h1,t); // differentiate h1
==> -20+80t-120t2+80t3-20t4
subst(h1,t,1); // substitute t by 1
==> 0
// The procedures T_1, T_2, T_12 may be called with two arguments and then
// they return a list with more information (type help T_1; etc.)
// e.g., T_12(i,<any>); returns a list with 9 nonempty objects where
// _[1] = std basis of T_1-module, _[2] = std basis of T_2-module,
// _[3]= vdim of T_1, _[4]= vdim of T_2
setring r1; // make r1 again the basering
list L = T_12(i,1);
==> // dim T_1 = 4
==> // dim T_2 = 3
kbase(L[1]); // kbase of T_1
==> _[1]=1*gen(2)
==> _[2]=1*gen(3)
==> _[3]=1*gen(6)
==> _[4]=1*gen(7)
kbase(L[2]); // kbase of T_2
==> _[1]=1*gen(6)
==> _[2]=1*gen(8)
==> _[3]=1*gen(9)
L[3]; // vdim of T_1
==> 4
L[4]; // vdim of T_2
==> 3
|
|