|
|
D.4.19.3 normalToricRingFromBinomials
Procedure from library normaliz.lib (see normaliz_lib).
- Usage:
- normalToricRingFromBinomials(ideal I);
normalToricRingFromBinomials(ideal I, intvec grading);
- Return:
- The ideal
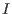 is generated by binomials of type is generated by binomials of type 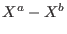 (multiindex notation)
in the surrounding polynomial ring (multiindex notation)
in the surrounding polynomial ring
![$K[X]=K[X_1,...,X_n]$](sing_950.png) . The binomials
represent a congruence on the monoid . The binomials
represent a congruence on the monoid 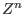 with residue monoid with residue monoid 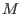 .
Let .
Let 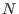 be the image of be the image of 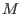 in gp( in gp(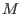 )/torsion. Then )/torsion. Then 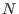 is universal in the
sense that every homomorphism from is universal in the
sense that every homomorphism from 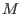 to an affine monoid factors through to an affine monoid factors through 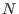 .
If .
If 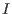 is a prime ideal, then is a prime ideal, then ![$K[N]= K[X]/I$](sing_952.png) . In general, . In general, ![$K[N]=K[X]/P$](sing_953.png) where where
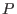 is the unique minimal prime ideal of is the unique minimal prime ideal of 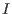 generated by binomials of type generated by binomials of type
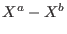 . .
The function computes the normalization of ![$K[N]$](sing_955.png) and returns a newly created
polynomial ring of the same Krull dimension, whose variables are and returns a newly created
polynomial ring of the same Krull dimension, whose variables are
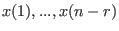 , where , where 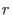 is the rank of the matrix with rows is the rank of the matrix with rows 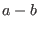 .
(In general there is no canonical choice for such an embedding.)
Inside this polynomial ring there is an ideal .
(In general there is no canonical choice for such an embedding.)
Inside this polynomial ring there is an ideal 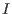 which lists the algebra
generators of the normalization of which lists the algebra
generators of the normalization of ![$K[N]$](sing_955.png) . .
The function returns the input ideal I if one of the options
supp, triang, volume, or hseries
has been activated.
However, in this case some numerical invariants are computed, and
some other data may be contained in files that you can read into
Singular (see showNuminvs, exportNuminvs).
Example:
| | LIB "normaliz.lib";
ring R = 37,(u,v,w,x,y,z),dp;
ideal I = u2v-xyz, ux2-wyz, uvw-y2z;
def S = normalToricRingFromBinomials(I);
setring S;
I;
==> I[1]=x(3)
==> I[2]=x(2)
==> I[3]=x(1)*x(3)^3
==> I[4]=x(1)*x(2)*x(3)^2
==> I[5]=x(1)*x(2)^2*x(3)
==> I[6]=x(1)*x(2)^3
==> I[7]=x(1)^2*x(2)^3*x(3)^2
==> I[8]=x(1)^2*x(2)^4*x(3)
==> I[9]=x(1)^3*x(2)^5*x(3)^2
|
See also:
ehrhartRing;
intclMonIdeal;
intclToricRing;
normalToricRing.
|