4.13 module
Modules are submodules of a free module over the basering with basis
gen(1), gen(2), ... .
They are represented by lists of vectors which generate the submodule.
Like vectors they
can only be defined or accessed with respect to a basering.
If
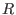 is the basering, and is the basering, and
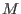 is a submodule of is a submodule of
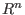
generated by vectors
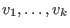 , then , then
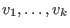
may be considered as the generators of relations of
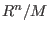 between the
canonical generators between the
canonical generators gen(1),...,gen(n). Hence any finitely
generated
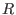 -module can be represented in SINGULAR by its module
of relations. The assignments -module can be represented in SINGULAR by its module
of relations. The assignments module M=v1,...,vk; matrix A=M; create
the presentation matrix of size n
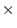 k for k for
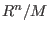 , i.e., the
columns of A are the vectors , i.e., the
columns of A are the vectors
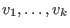 which generate M (cf.
Representation of mathematical objects). which generate M (cf.
Representation of mathematical objects).
|