|
|
7.3.1 betti (plural)
Syntax:
betti ( list_expression )
betti ( resolution_expression )
betti ( list_expression , int_expression )
betti ( resolution_expression , int_expression )
Type:
- intmat
Note:
- in the non-commutative case, computing Betti numbers makes sense only if the basering
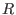 has homogeneous relations.
The output of the command can be pretty-printed using has homogeneous relations.
The output of the command can be pretty-printed using print( , "betti"), i.e., with "betti" as second argument; see below example.
Purpose:
- with 1 argument: computes the graded Betti numbers of a minimal resolution of
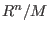 , if , if 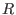 denotes the basering and denotes the basering and
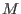 a homogeneous submodule of a homogeneous submodule of 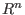 and the argument represents a
resolution of and the argument represents a
resolution of
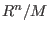 . .
The entry d of the intmat at place (i, j) is the minimal number of
generators in degree i+j of the j-th syzygy module (= module of
relations) of 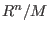 (the 0th (resp. 1st) syzygy module of (the 0th (resp. 1st) syzygy module of 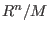 is is
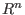 (resp. (resp. 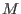 )).The argument is considered to be the result of a )).The argument is considered to be the result of a mres or nres
command. This implies that a zero is only allowed (and counted) as a
generator in the first module.
For the computation betti uses only the initial monomials. This could lead to confusing results for a non-homogeneous input.
If the optional second argument is non-zero, the Betti numbers will be minimized.
Example:
| | int i;int N=2;
ring r=0,(x(1..N),d(1..N),q(1..N)),Dp;
matrix D[3*N][3*N];
for (i=1;i<=N;i++)
{ D[i,N+i]=q(i)^2; }
def W=nc_algebra(1,D); setring W;
// this algebra is a kind of homogenized Weyl algebra
W;
==> // coefficients: QQ
==> // number of vars : 6
==> // block 1 : ordering Dp
==> // : names x(1) x(2) d(1) d(2) q(1) q(2)
==> // block 2 : ordering C
==> // noncommutative relations:
==> // d(1)x(1)=x(1)*d(1)+q(1)^2
==> // d(2)x(2)=x(2)*d(2)+q(2)^2
ideal I = x(1),x(2),d(1),d(2),q(1),q(2);
option(redSB);
option(redTail);
resolution R = mres(I,0);
// thus R will be the full length minimal resolution
print(betti(R),"betti");
==> 0 1 2 3 4 5 6
==> ------------------------------------------------
==> 0: 1 6 15 20 15 6 1
==> ------------------------------------------------
==> total: 1 6 15 20 15 6 1
==>
|
|