|
|
7.9.1 Free associative algebras
Let
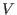 be a be a
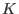 -vector space, spanned by the symbols -vector space, spanned by the symbols
 ,..., ,...,
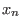 .
A free associative algebra in .
A free associative algebra in
 ,..., ,...,
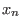 over over
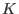 , denoted by , denoted by
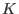
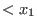 ,..., ,...,
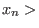
is also known as the tensor algebra
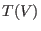 of of
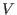 ;
it is also the monoid ;
it is also the monoid
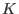 -algebra of the free monoid -algebra of the free monoid
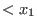 ,..., ,...,
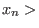 .
The elements of this free monoid constitute an infinite .
The elements of this free monoid constitute an infinite
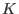 -basis of -basis of
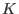
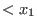 ,..., ,...,
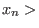 ,
where the identity element (the empty word) of the free monoid is identified with the ,
where the identity element (the empty word) of the free monoid is identified with the
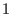 in in
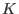 .
Yet in other words, the monomials of .
Yet in other words, the monomials of
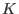
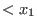 ,..., ,...,
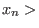 are the words
of finite length in the finite alphabet { are the words
of finite length in the finite alphabet {
 ,..., ,...,
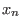 }. }.
The algebra
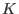
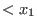 ,..., ,...,
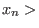 is an integral domain, which is not (left, right, weak or two-sided) Noetherian for is an integral domain, which is not (left, right, weak or two-sided) Noetherian for
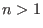 ; hence, a Groebner basis of a finitely generated ideal might be infinite.
Therefore, a general computation takes place up to an explicit degree (length) bound, provided by the user.
The free associative algebra can be regarded as a graded algebra in a natural way. ; hence, a Groebner basis of a finitely generated ideal might be infinite.
Therefore, a general computation takes place up to an explicit degree (length) bound, provided by the user.
The free associative algebra can be regarded as a graded algebra in a natural way.
Definition. An associative algebra
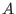 is called finitely presented (f.p.), if it is isomorphic to is called finitely presented (f.p.), if it is isomorphic to
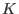
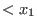 ,..., ,...,
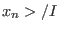 ,
where ,
where
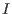 is a two-sided ideal. is a two-sided ideal.
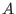 is called standard finitely presented (s.f.p.), if there exists a monomial ordering,
such that is called standard finitely presented (s.f.p.), if there exists a monomial ordering,
such that
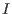 is given via its finite Groebner basis is given via its finite Groebner basis
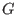 . .
|