7.9.3 Groebner bases for two-sided ideals in free associative algebras
We say that a monomial
 divides (two-sided or bilaterally) a monomial divides (two-sided or bilaterally) a monomial
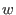 , if there exist monomials , if there exist monomials
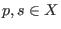 , such that , such that
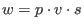 , in other words , in other words
 is a subword of is a subword of
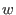 . .
For a subset
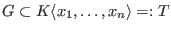 ,
define the leading ideal of ,
define the leading ideal of 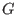 to be the two-sided ideal to be the two-sided ideal
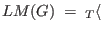
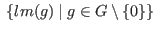
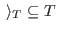 . .
Let 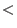 be a fixed monomial ordering on be a fixed monomial ordering on 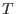 .
We say that a subset .
We say that a subset 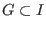 is a (two-sided) Groebner basis for the ideal is a (two-sided) Groebner basis for the ideal 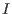 with respect to with respect to 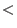 , if , if 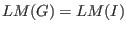 . That is . That is
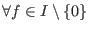 there exists there exists 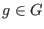 , such that , such that
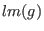 divides divides 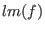 . .
Suppose, that the weights of the ring variables are strictly positive.
We can interprete these weights as defining a nonstandard grading on the ring.
If the set of input polynomials is weighted homogeneous with respect to the given
weights of the ring variables, then computing up to a weighted degree (and thus, also length) bound
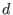
results in the truncated Groebner basis
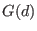 . In other words, by trimming elements
of degree exceeding . In other words, by trimming elements
of degree exceeding
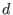 from the complete Groebner basis from the complete Groebner basis
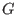 , one obtains precisely , one obtains precisely
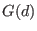 . .
In general, given a set
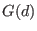 , which is the result of Groebner basis computation
up to weighted degree bound , which is the result of Groebner basis computation
up to weighted degree bound
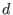 , then
it is the complete finite Groebner basis, if and only if , then
it is the complete finite Groebner basis, if and only if
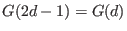 holds. holds.
|