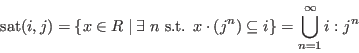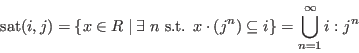|
|
A.3.1 Saturation
For any two ideals
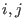 in the basering in the basering
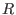 let let
denote the saturation of
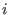 with respect to with respect to
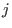 . This defines,
geometrically, the closure of the complement of V( . This defines,
geometrically, the closure of the complement of V(
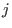 ) in V( ) in V(
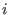 )
(where V( )
(where V(
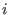 ) denotes the variety defined by ) denotes the variety defined by
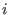 ). ).
The saturation is computed by the procedure sat in
elim.lib by computing iterated ideal quotients with the maximal
ideal. sat returns a list of two elements: the saturated ideal
and the number of iterations.
We apply saturation to show that a variety has no singular points
outside the origin (see also Critical points).
We choose
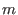 to be the homogeneous maximal ideal
(note that to be the homogeneous maximal ideal
(note that maxideal(n) denotes the n-th power of the maximal
ideal).
Then
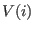 has no singular point outside the origin
if and only if has no singular point outside the origin
if and only if
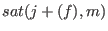 is the whole ring, that is, generated by 1. is the whole ring, that is, generated by 1.
| | LIB "elim.lib"; // loading library elim.lib
ring r2 = 32003,(x,y,z),dp;
poly f = x^11+y^5+z^(3*3)+x^(3+2)*y^(3-1)+x^(3-1)*y^(3-1)*z3+
x^(3-2)*y^3*(y^2)^2;
ideal j=jacob(f);
sat(j+f,maxideal(1));
==> [1]:
==> _[1]=1
==> [2]:
==> 17
// list the variables defined so far:
listvar();
==> // r2 [0] *ring
==> // j [0] ideal, 3 generator(s)
==> // f [0] poly
|
|