B.2.2 General definitions for orderings
A monomial ordering (term ordering) on
![$K[x_1,\ldots,x_n]$](sing_60.png) is
a total ordering is
a total ordering 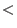 on the
set of monomials (power products) on the
set of monomials (power products)
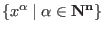 which is compatible with the
natural semigroup structure, i.e.,
which is compatible with the
natural semigroup structure, i.e.,
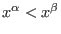 implies implies
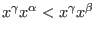 for any for any
 .
We do not require .
We do not require
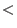 to be a wellordering. See the literature cited in References. to be a wellordering. See the literature cited in References.
It is known that any monomial ordering can be represented by a matrix
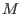 in in 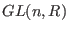 ,but, of course, only integer coefficients are of relevance in
practice. ,but, of course, only integer coefficients are of relevance in
practice.
Global orderings are wellorderings (i.e., 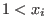 for each variable for each variable
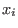 ), local orderings satisfy ), local orderings satisfy 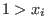 for each variable. If some variables are ordered globally and others locally we
call it a mixed ordering. Local or mixed orderings are not wellorderings. for each variable. If some variables are ordered globally and others locally we
call it a mixed ordering. Local or mixed orderings are not wellorderings.
Let 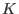 be the ground field, be the ground field,
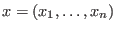 the
variables and the
variables and 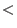 a monomial ordering, then Loc a monomial ordering, then Loc ![$K[x]$](sing_512.png) denotes the
localization of denotes the
localization of ![$K[x]$](sing_512.png) with respect to the multiplicatively closed set with respect to the multiplicatively closed set
Here, 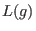 denotes the leading monomial of
denotes the leading monomial of 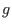 , i.e., the biggest monomial of , i.e., the biggest monomial of 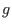 with
respect to with
respect to 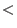 . The result of any computation which uses standard basis
computations has to be interpreted in Loc . The result of any computation which uses standard basis
computations has to be interpreted in Loc ![$K[x]$](sing_512.png) . .
Note that the definition of a ring includes the definition of its
monomial ordering (see
Rings and orderings). SINGULAR offers the monomial orderings
described in the following sections.
|
 Online Manual
Online Manual