C.6.2.3 The algorithm of Hosten and Sturmfels
The algorithm of Hosten and Sturmfels (see [HoSt95]) allows to
compute 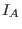 without any auxiliary variables, provided that without any auxiliary variables, provided that 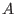 contains a vector contains a vector 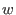 with positive coefficients in its row space. This is a real restriction,
i.e., the algorithm will not necessarily work in the general case.
with positive coefficients in its row space. This is a real restriction,
i.e., the algorithm will not necessarily work in the general case.
A lattice basis
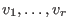 is again computed via the
LLL-algorithm.
The saturation step is performed in the following way:
First note that is again computed via the
LLL-algorithm.
The saturation step is performed in the following way:
First note that 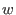 induces a positive grading w.r.t. which the ideal induces a positive grading w.r.t. which the ideal
is homogeneous corresponding to our lattice basis. We use the following
lemma:
Let 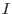 be a homogeneous ideal w.r.t. the weighted reverse
lexicographical ordering with weight vector be a homogeneous ideal w.r.t. the weighted reverse
lexicographical ordering with weight vector 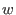 and variable order and variable order
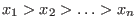 . Let . Let 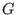 denote a Groebner basis of denote a Groebner basis of 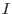 w.r.t.
this ordering. Then a Groebner basis of w.r.t.
this ordering. Then a Groebner basis of
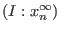 is obtained by
dividing each element of is obtained by
dividing each element of 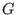 by the highest possible power of by the highest possible power of 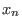 . .
From this fact, we can succesively compute
in the 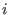 -th step we take -th step we take 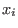 as the smallest variable and apply the
lemma with as the smallest variable and apply the
lemma with 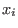 instead of instead of 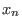 . .
This procedure involves 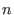 Groebner basis computations. Actually, this
number can be reduced to at most Groebner basis computations. Actually, this
number can be reduced to at most 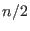 (see [HoSh98]), and each computation -- except for the first one --
proves to be simple and fast in practice. (see [HoSh98]), and each computation -- except for the first one --
proves to be simple and fast in practice.
|
 Online Manual
Online Manual