|
|
B.2.4 Local orderings
For ls, ds, Ds and, if the weights are positive integers, also for ws and
Ws, we have
Loc ![$K[x]$](sing_549.png) = = ![$K[x]_{(x)}$](sing_562.png) , the localization of , the localization of
![$K[x]$](sing_549.png) at the maximal ideal at the maximal ideal
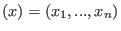 . .
- ls:
- negative lexicographical ordering:
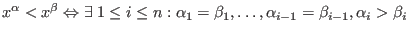 . . - ds:
- negative degree reverse lexicographical ordering:
let
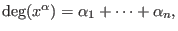 then then
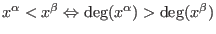 or or
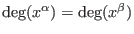 and and
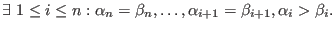 - Ds:
- negative degree lexicographical ordering:
let
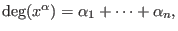 then then
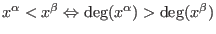 or or
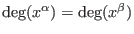 and and
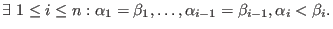 - ws:
- (general) weighted reverse lexicographical ordering:
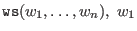 a nonzero integer, a nonzero integer,
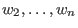 any integer (including 0),
is defined as any integer (including 0),
is defined as ds
but with
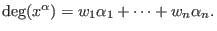 - Ws:
- (general) weighted lexicographical ordering:
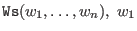 a nonzero integer, a nonzero integer,
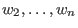 any integer (including 0),
is defined as any integer (including 0),
is defined as Ds
but with
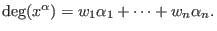
|