| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
7.1 PLURAL

A Subsystem for Non-commutative Polynomial G-Algebras
- What is and what does PLURAL?
PLURAL is a kernel extension of SINGULAR, providing many algorithms for computations within non-commutative
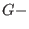 and
and
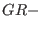 algebras
(see Mathematical background (plural) for detailed information on algebras and algorithms).
algebras
(see Mathematical background (plural) for detailed information on algebras and algorithms).
It uses the same data structures as SINGULAR, sometimes interpreting them in a different way and/or modifying them for its own purposes. In spite of such a difference, one can always transfer objects between commutative rings of SINGULAR and non-commutative rings of PLURAL.
With PLURAL, one can set up a non-commutative
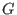 -algebra, say
-algebra, say
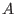 , with
a Poincaré-Birkhoff-Witt (PBW) basis, (see G-algebras for step-by-step building instructions
and also PLURAL libraries for procedures for setting many important algebras easily).
Afterwards, one can proceed to the factor-algebra of
, with
a Poincaré-Birkhoff-Witt (PBW) basis, (see G-algebras for step-by-step building instructions
and also PLURAL libraries for procedures for setting many important algebras easily).
Afterwards, one can proceed to the factor-algebra of
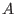 modulo a two-sided ideal (see twostd (plural)), thus
obtaining a
modulo a two-sided ideal (see twostd (plural)), thus
obtaining a
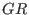 -algebra (see qring (plural) type).
-algebra (see qring (plural) type).
Functionalities of PLURAL (enlisted in Functions (plural)) are accessible as soon as the basering becomes non-commutative (see nc_algebra and the library ncalg_lib with many readily predefined algebras).
One can perform various computations with polynomials and ideals in
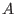 and with
vectors and submodules of a free module
and with
vectors and submodules of a free module
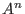 .
.
- What PLURAL does not:
-
PLURAL does not perform computations in the free algebra or in its general factor algebras
(instead, these computations can be possibly done by LETTERPLACE).
In PLURAL one can only work with
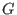 -algebras and with their factor-algebras
by two-sided ideals (
-algebras and with their factor-algebras
by two-sided ideals (
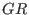 -algebras).
-algebras).
- PLURAL requires a global monomial ordering (see General definitions for orderings).
However, SCA ( Graded commutative algebras (SCA)) provides the possibility of computations in a tensor product of
a non-commutative graded commutative algebra (equipped with a global ordering)
with a commutative algebra (equipped with any ordering).
- PLURAL does not handle non-commutative parameters, i.e. the elements of
the coefficient field (or a ring) mutually commute with all variables.
Defining parameters, one cannot impose non-commutative relations
on them. Moreover, it is impossible to introduce parameters which do not commute with variables.
However, olga_lib offers a rich functionality for working within Ore localizations of
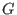 -algebras
and ratgb_lib provides Groebner bases for so-called rational localizations of
-algebras
and ratgb_lib provides Groebner bases for so-called rational localizations of
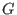 -algebras.
-algebras.
- PLURAL does not yet support rings like
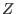 as coefficients.
as coefficients.
-
PLURAL does not perform computations in the free algebra or in its general factor algebras
(instead, these computations can be possibly done by LETTERPLACE).
- PLURAL conventions
- *-multiplication (plural)
in the non-commutative case, the correct multiplication of
ybyxmust be written asy*x.
Both expressionsyxandxyare equal, since they are interpreted as commutative expressions. See example in poly expressions (plural).
Note, that PLURAL output consists only of standard monomials, even when the signs*are omitted.ideal(plural)Unless stated otherwise, an expression of type
idealas understood by PLURAL as a list of generators of a left ideal. For more information see ideal (plural).
For a two-sided idealT, use the command twostd (plural) for computing the two-sided Groebner basis ofT.
For a right idealI, use rightstd (letterplace) fromnctools_libfor computing the right Groebner basis ofI.module(plural)- Unless stated otherwise, a
moduleas understood by PLURAL is either a finitely generated left submodule of a free module (of finite rank)
or a factor module of a free module (of finite rank) by its left submodule (see module (plural) for details). The concrete interpretation left to a function. qring(plural)- It is only possible to build factor-algebras modulo two-sided ideals (see qring (plural)), which have to be given via their two-sided Groebner basis (see twostd (plural)).