|
|
4.6.4 ideal related functions
char_series
- irreducible characteristic series (see char_series)
coeffs
- matrix of coefficients (see coeffs)
contract
- contraction by an ideal (see contract)
diff
- partial derivative (see diff)
degree
- multiplicity, dimension and codimension of the ideal of leading terms (see degree)
dim
- Krull dimension of basering modulo the ideal of leading terms (see dim)
eliminate
- elimination of variables (see eliminate)
facstd
- factorizing Groebner basis algorithm (see facstd)
factorize
- ideal of factors of a polynomial (see factorize)
fglm
- Groebner basis computation from a Groebner basis w.r.t. a different
ordering (see fglm)
finduni
- computation of univariate polynomials lying in a zero dimensional ideal
(see finduni)
fres
- free resolution of a standard basis (see fres)
groebner
- Groebner basis computation (a wrapper around
std,stdhilb,stdfglm,...)
(see groebner)
highcorner
- the smallest monomial not contained in the ideal.
The ideal has to be zero-dimensional.
(see highcorner)
homog
- homogenization with respect to a variable (see homog)
hilb
- Hilbert series of a standard basis (see hilb)
indepSet
- sets of independent variables of an ideal (see indepSet)
interred
- interreduction of an ideal (see interred)
intersect
- ideal intersection (see intersect)
jacob
- ideal of all partial derivatives resp. jacobian matrix (see jacob)
jet
- Taylor series up to a given order (see jet)
kbase
- vector space basis of basering modulo ideal of leading terms
(see kbase)
koszul
- Koszul matrix (see koszul)
lead
- leading terms of a set of generators (see lead)
lift
- lift-matrix (see lift)
liftstd
- standard basis and transformation matrix computation (see liftstd)
lres
- free resolution for homogeneous ideals (see lres)
maxideal
- power of the maximal ideal at 0 (see maxideal)
minbase
- minimal generating set of a homogeneous ideal, resp. module, or an ideal, resp. module, in a local ring
(see minbase)
minor
- set of minors of a matrix (see minor)
modulo
- representation of
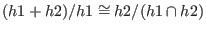 (see modulo) (see modulo)
mres
- minimal free resolution of an ideal resp. module w.r.t. a minimal set of generators of the given ideal resp. module
(see mres)
mstd
- standard basis and minimal generating set of an ideal (see mstd)
mult
- multiplicity, resp. degree, of the ideal of leading terms (see mult)
ncols
- number of columns (see ncols)
nres
- a free resolution of an ideal resp. module M which is
minimized from the second free module on (see nres)
preimage
- preimage under a ring map (see preimage)
qhweight
- quasihomogeneous weights of an ideal (see qhweight)
quotient
- ideal quotient (see quotient)
reduce
- normalform with respect to a standard basis (see reduce)
res
- free resolution of an ideal resp. module but not changing the given ideal resp. module
(see res)
simplify
- simplification of a set of polynomials (see simplify)
size
- number of non-zero generators (see size)
slimgb
- Groebner basis computation with slim technique (see slimgb)
sortvec
- permutation for sorting ideals resp. modules (see sortvec)
sres
- free resolution of a standard basis (see sres)
std
- standard basis computation (see std)
stdfglm
- standard basis computation with fglm technique (see stdfglm)
stdhilb
- Hilbert driven standard basis computation (see stdhilb)
subst
- substitution of a ring variable (see subst)
syz
- computation of the first syzygy module (see syz)
vdim
- vector space dimension of basering modulo ideal of leading terms
(see vdim)
weight
- optimal weights (see weight)
|



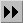





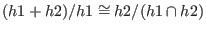 (see modulo)
(see modulo)